Mathematics and Computation

In 1890 Giuseppe Peano discovered a square-filling curve, and a year later David Hilbert published his variation. In those days people did not waste readers' attention with dribble – Peano explained it all on 3 pages, and Hilbert on just 2 pages, with a picture!

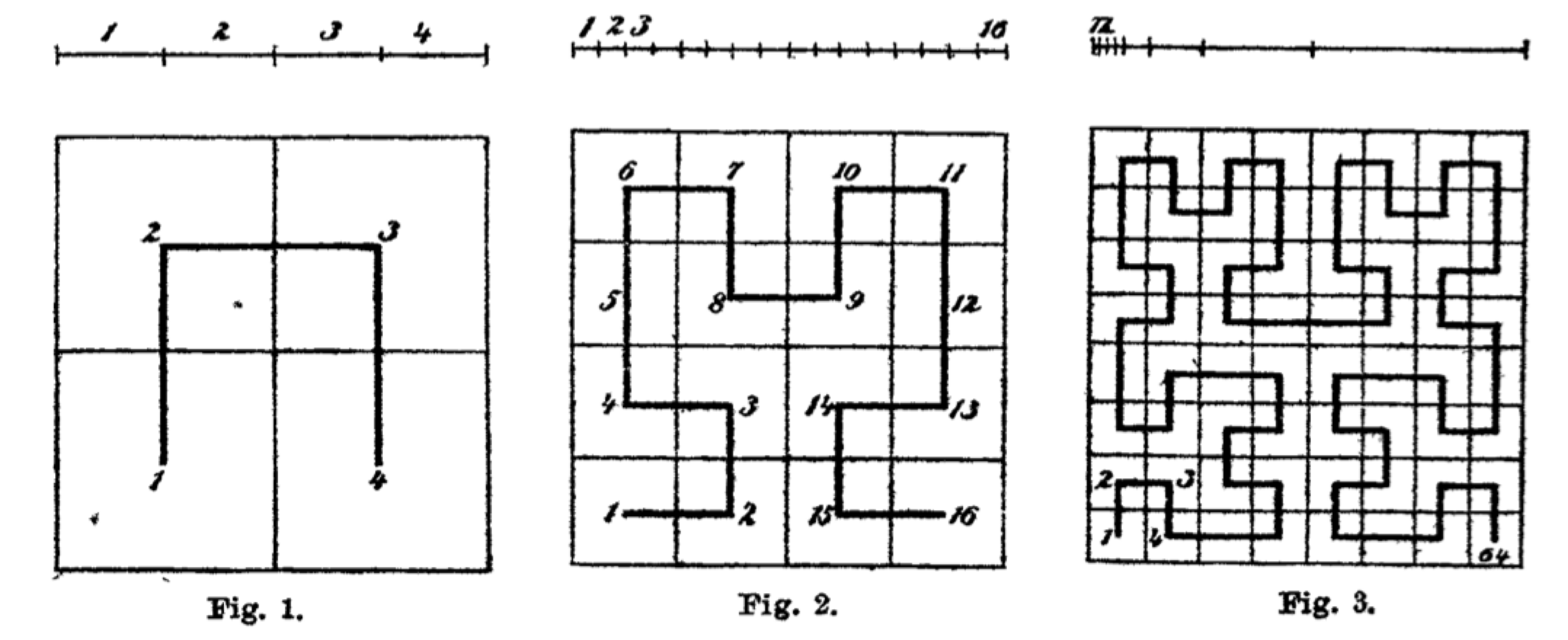
But are these constructive square-filling curves?

→ continue reading

In a discussion following a MathOverflow answer by Joel Hamkins, Timothy Chow and I got into a chat about what it means for a statement to “not have a definite truth value”. I need a break from writing the paper on countable reals (coming soon in a journal near you), so I thought it would be worth writing up my view of the matter in a blog post.

→ continue reading

I gave a talk “Variations on Weihrauch degrees” at Computability in Europe 2023, which took place in Tbilisi, Georgia. The talk was a remote one, unfortunately. I spoke about generalizations of Weihrauch degrees, a largely unexplored territory that seems to offer many opportunities to explore new directions of research. I am unlikely to pursue them myself, but will gladly talk with anyone who is interested in doing so.

Slides: CiE-2023-slides.pdf.

→ continue reading

On the occasion of Dieter Spreen's 75th birthday there will be a Festschrift in the Journal of Logic and Analysis. I have submitted a paper “Spreen spaces and the synthetic Kreisel-Lacombe-Shoenfield-Tseitin theorem”, available as a preprint arXiv:2307.07830, that develops a constructive account of Dieter's generalization of a famous theorem about continuity of computable functions. In this post I explain how the paper fits into the more general topic of continuity principles.

→ continue reading

At TYPES 2023 I had the honor of giving an invited talk “On Isomorphism Invariance and Isomorphism Reflection in Type Theory” in which I discussed isomorphism reflection, which states that isomorphic types are judgementally equal. This strange principle is consistent, and it validates some fairly strange type-theoretic statements.

Here are the slides with speaker notes and the video recording of the talk.

→ continue reading

I am at the Machine assisted proofs workshop at the UCLA Institute for Pure and Applied Mathematics, where I am about to give a talk on “Formalizing invisible mathematics”.

Here are the slides with speaker notes and the video recording of the talk.

→ continue reading

On February 10, 2023, I gave my Levi L. Conant Lectur Series talk “Exploring strange new worlds of mathematics”, at the math department of Worcester Polytechnic Institute. Here are the slides with speaker notes and the video recording of the talk.

→ continue reading

Today Dana Scott is celebrating the 90th birthday today. Happy birthday, Dana! I am forever grateful for your kindness and the knowledge that I received from you. I hope to pass at least a part of it onto my students.

On the occasion Steve Awodey assembled selected works by Dana Scott at CMU-HoTT/scott repository. It is an amazing collection of papers that had deep impact on logic, set theory, computation, and programming languages. I hope in the future we can extend it and possibly present it in better format.

As a special treat, I recount here the story the invention of the famous $D_\infty$ model of the untyped $\lambda$-calculus. I heard it first when I was Dana's student. In 2008 I asked Dana to recount it in the form of a short interview.

→ continue reading (1 comment)

I am at the Syntax and Semantics of Type Theory workshop in Stockholm, a kickoff meeting for WG6 of the EuroProofNet COST network, where I am giving a talk “One syntax to rule them all” based on joint work with Danel Ahman.

→ continue reading

Within a month two of my students defended their theses: Dr. Anja Petković Komel just before Christmas, and Dr. Philipp Haselwarter just yesterday. I am very proud of them. Congratulations!

→ continue reading

Jacques Carette asked on Twitter for a refence to the fact that countable choice holds in setoids. I then spent a day formalizing facts about the axiom of choice in setoids in Agda. I noticed something interesting that is worth blogging about.

→ continue reading (4 comments)

Proof assistant communities have grown quite a bit lately. They have active Zulip chats: Lean, Coq, Agda, Isabelle. These are good for discussions, but less so for knowledge accumulation and organization, and are not indexed by the search engines.

I have therefore created a proposal for a new “Proof assistants” StackExchange site. I believe that such a site would complement very well various Zulips dedicated to specific proof assistants. If you favor the idea, please support it by visiting the proposal and

• becoming a follower (you have to be a registered user with a verified email account),
• asking sample questions, and
• upvoting good sample questions.

To pass the first stage, we need 60 followers and 40 questions with at least 10 votes to proceed to the next stage.

→ continue reading (2 comments)

Here are the slides of my talk "The dawn of formalized mathematics" from the 8th European Congress of Mathematics, which is taking place online and in Protorož, Slovenia, from June 20 to 26, 2021:

• Keynote presentation, viewable online in your browser. Turn on the speaker notes by clicking on the rectangular icon in the top-left corner.
• Slides with speaker notes (PDF). Unfortunately, Keynote does not make the hyperlinks active when exporting PDF.
• Video recording of the talk.

→ continue reading (3 comments)

A while ago, my former student Chuangjie Xu and I computed an integer using a sheaf topos. For that purpose,

1. we developed our mathematics constructively,
2. we formalized our mathematics in Martin-Löf type theory, in Agda notation,
3. we pressed a button, and
4. after a few seconds we saw the integer we expected in front of us.

Well, it was a few seconds for the computer in steps (3)-(4), but three years for us in steps (1)-(2).

→ continue reading

This is joint work with Marc Bezem, Thierry Coquand, Peter Dybjer.

We use the Burali-Forti argument to show that, in homotopy type theory and univalent foundations, the embedding $$ \mathcal{U} \to \mathcal{U}^+$$ of a universe $\mathcal{U}$ into its successor $\mathcal{U}^+$ is not an equivalence. We also establish this for the types of sets, magmas, monoids and groups. The arguments in this post are also written in Agda.

→ continue reading

It is my pleasure to have the opportunity to speak at the University of Wisconsin Logic seminar. The hosts are graciously keeping the seminar open for everyone. I will speak about a favorite topic of mine, synthetic computability.

→ continue reading

After a short pause, our next talk in the series will be given by Jamie Vicary, who will present a proof assistant in which the proofs are drawn!

Introducing homotopy.io: A proof assistant for geometrical higher category theory

Time: Thursday, November 26, 2020 from 15:00 to 16:00 (Central European Time, UTC+1)
Location: online at Zoom ID 989 0478 8985
Speaker: Jamie Vicary (University of Cambridge)
Proof assistant: homotopy.io

Abstract:

Weak higher categories can be difficult to work with algebraically, with the weak structure potentially leading to considerable bureaucracy. Conjecturally, every weak infty-category is equivalent to a "semistrict" one, in which unitors and associators are trivial; such a setting might reduce the burden of constructing large proofs. In this talk, I will present the proof assistant homotopy.io, which allows direct construction of composites in a finitely-generated semistrict (infty,infty)-category. The terms of the proof assistant have a geometrical interpretation as string diagrams, and interaction with the proof assistant is entirely geometrical, by clicking and dragging with the mouse, completely unlike more traditional computer algebra systems. I will give an outline of the underlying theoretical foundations, and demonstrate use of the proof assistant to construct some nontrivial homotopies, rendered in 2d and 3d. I will close with some speculations about the possible interaction of such a system with more traditional type-theoretical approaches. (Joint work with Lukas Heidemann, Nick Hu and David Reutter.)

References:

• David Reutter, Jamie Vicary: High-level methods for homotopy construction in associative n-categories, arXiv:1902.03831 preprint, February 2019.
• homotopy.io at Lab

→ continue reading

The preprint version of the paper A general definition of dependent type theories has finally appeared on the arXiv! Over three years ago Peter Lumsdaine invited me to work on the topic, which I gladly accepted, and dragged my student Philipp Haselwarter into it. We set out to give an answer to the queation:

What is type theory, precisely?

At least for me the motivation to work on such a thankless topic came from Vladimir Voevodsky, who would ask the question to type-theoretic audiences. Some took him to be a troll and others a newcomer who just had to learn more type theory. I was among the latter, but eventually the question got through to me – I could point to any number of specific examples of type theories, but not a comprehensive and mathematically precise definition of the general concept.

It is too easy to dismiss the question by claiming that type theory is an open-ended concept which therefore cannot be completely captured by any mathematical definition. Of course it is open-ended, but it does not follow at all that we should not even attempt to define it. If geometers were equally fatalistic about the open-ended notion of space we would never have had modern geometry, topology, sheaves – heck, half of 20th century mathematics would not be there!

Of course, we are neither the first nor the last to give a definition of type theory, and that is how things should be. We claim no priority or supremacy over other definitions and views of type theory. Our approach could perhaps be described as "concrete" and "proof-theoretic":

1. We wanted to stay close to traditional syntax.
2. We gave a complete and precise definition.
3. We aimed for a level of generality that allows useful meta-theory of a wide range of type theories.

One can argue each of the above points, and we have done so among ourselves many times. Nevertheless, I feel that we have accomplished something worthwhile – but the ultimate judges will be our readers, or lack of them. You are kindly invited to take a look at the paper.

Download PDF: arxiv.org/pdf/2009.05539.pdf

I should not forget to mention that Peter, with modest help from Philipp and me, formalized almost the entire paper in Coq! See the repository general-type-theories at GitHub.

→ continue reading

I am happy to announce that we are restarting the "Every proof assistants" series of talks with Anders Mörtberg who will talk about Cubical Agda. Note that we are moving the seminar time to a more reasonable hour, at least as far as the working people in Europe are concerned.

Cubical Agda: A Dependently Typed Programming Language with Univalence and Higher Inductive Types

Time: Thursday, September 17, 2020 from 15:00 to 16:00 (Central European Summer Time, UTC+2)
Location: online at Zoom ID 989 0478 8985
Speaker: Anders Mörtberg (Stockholm University)
Proof assistant: Cubical Agda

Abstract: The dependently typed programming language Agda has recently been extended with a cubical mode which provides extensionality principles for reasoning about equality, such as function and propositional extensionality. These principles are typically added axiomatically to proof assistants based on dependent type theory which disrupts the constructive properties of these systems. Cubical type theory provides a solution by giving computational meaning to Homotopy Type Theory and Univalent Foundations, in particular to the univalence axiom and higher inductive types. In the talk I will discuss how Agda was extended to a full-blown proof assistant with native support for univalence and a general schema of higher inductive types. I will also show a variety of examples of how to use Cubical Agda in practice to reason about mathematics and computer science.

The talk video recording is available.

We have more talks in store, but we will space them out a bit to give slots to our local seminar.

→ continue reading

We shall finish the semester with a "Every proof assistant" talk by William Bowman. Note that we start an hour later than usual, at 17:00 UTC+2.

Cur: Designing a less devious proof assistant

Time: Thursday, June 25, 2020 from 17:00 to 18:00 (Central European Summer Time, UTC+2)
Location: online at Zoom ID 989 0478 8985
Speaker: William J. Bowman (University of British Columbia)
Proof assistant: Cur

Abstract:

Dijkstra said that our tools can have a profound and devious influence on our thinking. I find this especially true of modern proof assistants, with "devious" out-weighing "profound". Cur is an experiment in design that aims to be less devious. The design emphasizes language extension, syntax manipulation, and DSL construction and integration. This enables the user to be in charge of how they think, rather than requiring the user to contort their thinking to that of the proof assistant. In this talk, my goal is to convince you that you want similar capabilities in a proof assistant, and explain and demonstrate Cur's attempt at solving the problem.

The talk video recording and slides with notes and demo code are available.

Upcoming talks: Anders Mörtberg's talk on Cubical Agda will take place in September 2020.

→ continue reading

This week shall witness a performance by Conor McBride.

Epigram 2: Autopsy, Obituary, Apology

Time: Thursday, June 11, 2020 from 16:00 to 17:00 (Central European Summer Time, UTC+2)
Location: online at Zoom ID 989 0478 8985
Speaker: Conor McBride (University of Strathclyde)
Proof assistant: Epigram 2

Abstract: "A good pilot is one with the same number of take-offs and landings." runs the old joke, which makes me a very bad pilot indeed. The Epigram 2 project was repeatedly restarted several times in the late 2000s and never even reached cruising altitude. This talk is absolutely not an attempt to persuade you to start using it. Rather, it is an exploration of the ideas which drove it: proof irrelevant observational equality, first class datatype descriptions, nontrivial equational theories for neutral terms. We may yet live to see such things. Although the programming language elaborator never happened, the underlying proof engine was accessible via an imperative interface called "Cochon": we did manage some interesting constructions, at least one of which I can walk through. I'll also explore the reasons, human and technological, why the thing did not survive the long dark.

The video recording of the talk.

Upcoming talks:

• June 25, 2020: William J. Bowman, Cur
• July 2, 2020: Anders Mörtberg - Cubical Agda

→ continue reading

This week the speaker will be Jon Sterling, and we are getting two proof assistants for the price of one!

redtt and the future of Cartesian cubical type theory

Time: Thursday, June 4, 2020 from 16:00 to 17:00 (Central European Summer Time, UTC+2)
Location: online at Zoom ID 989 0478 8985
Speaker: Jon Sterling (Carnegie Mellon University)
Proof assistant: redtt and cooltt

Abstract: redtt is an interactive proof assistant for Cartesian cubical type theory, a version of Martin-Löf type theory featuring computational versions of function extensionality, higher inductive types, and univalence. Building on ideas from Epigram, Agda, and Idris, redtt introduces a new cubical take on interactive proof development with holes. We will first introduce the basics of cubical type theory and then dive into an interactive demonstration of redtt’s features and its mathematical library.

After this we will catch a first public glimpse of the future of redtt, a new prototype that our team is building currently code-named “cooltt”: cooltt introduces syntax to split on disjunctions of cofibrations in arbitrary positions, implementing the full definitional eta law for disjunction. While cooltt is still in the early stages, it already has full support for univalence and cubical interactive proof development.

The video recording of the talk.

Upcoming talks:

• June 11, 2020: Conor McBride - Epigram 2
• June 25, 2020: William J. Bowman, Cur
• July 2, 2020: Anders Mörtberg - Cubical Agda

→ continue reading

We are marching on with the Every proof assistant series!

Mechanizing Meta-Theory in Beluga

Time: Thursday, May 28, 2020 from 16:00 to 17:00 (Central European Summer Time, UTC+2)
Location: online at Zoom ID 989 0478 8985
Speaker: Brigitte Pientka (McGill University)
Proof assistant: Beluga

Abstract: Mechanizing formal systems, given via axioms and inference rules, together with proofs about them plays an important role in establishing trust in formal developments. In this talk, I will survey the proof environment Beluga. To specify formal systems and represent derivations within them, Beluga relies on the logical framework LF; to reason about formal systems, Beluga provides a dependently typed functional language for implementing (co)inductive proofs about derivation trees as (co)recursive functions following the Curry-Howard isomorphism. Key to this approach is the ability to model derivation trees that depend on a context of assumptions using a generalization of the logical framework LF, i.e. contextual LF which supports first-class contexts and simultaneous substitutions.

Our experience demonstrated that Beluga enables direct and compact mechanizations of the meta-theory of formal systems, in particular programming languages and logics.

The video recording of the talk.

Upcoming talks:

• June 4, 2020: Jon Sterling - redtt
• June 11, 2020: Conor McBride - Epigram 2
• June 25, 2020: William J. Bowman, Cur
• July 2, 2020: Anders Mörtberg - Cubical Agda

→ continue reading

I am happy to announce the next seminar in the "Every proof assistant" series.

MMT: A Foundation-Independent Logical System

Time: Thursday, May 21, 2020 from 16:00 to 17:00 (Central European Summer Time, UTC+2)
Location: online at Zoom ID 989 0478 8985
Speaker: Florian Rabe (University of Erlangen)
Proof assistant: The MMT Language and System

Abstract: Logical frameworks are meta-logics for defining other logics. MMT follows this approach but abstracts even further: it avoids committing to any foundational features like function types or propositions. All MMT algorithms are parametric in a set of rules, which are self-contained objects plugged in by the language designer. That results in a framework general enough to develop many formal systems including other logical frameworks in it, enabling the rapidly prototyping of new language features.

Despite this high level of generality, it is possible to develop sophisticated results in MMT. The current release includes, e.g., parsing, type reconstruction, module system, IDE-style editor, and interactive library browser. MMT is systematically designed to be extensible, providing multiple APIs and plugin interfaces, and thus provides a versatile infrastructure for system development and integration.

This talk gives an overview of the current state of MMT and its future challenges. Examples are drawn from the LATIN project, a long-running project of building a modular, highly inter-related suite of formalizations of logics and related formal systems.

The video recording of the talk.

The spring schedule of talks is planned as follows:

• May 28, 2020: Brigitte Pientka - Beluga
• June 4, 2020: Jon Sterling - redtt (to be confirmed)
• June 11, 2020: Conor McBride - Epigram 2
• June 25, 2020: William J. Bowman, Cur
• July 2, 2020: Anders Mörtberg - Cubical Agda

→ continue reading (1 comment)

For a while now I have been contemplating a series of seminars titled "Every proof assistant" that would be devoted to all the different proof assistants out there. Apart from the established ones (Isabelle/HOL, Coq, Agda, Lean), there are other interesting experimental proof assistants, and some that are still under development, or just proofs of concept. I would like to know more about them, and I suspect I am not the only one.

→ continue reading (10 comments)

I forgot to record the fact that already two years ago I wrote a paper on Lawvere's fixed-point theorem in synthetic computability:

Andrej Bauer: On fixed-point theorems in synthetic computability. Tbilisi Mathematical Journal, Volume 10: Issue 3, pp. 167–181.

It was a special issue in honor of Professors Peter J. Freyd and F. William Lawvere on the occasion of their 80th birthdays.

Lawvere's paper "Diagonal arguments and cartesian closed categories proves a beautifully simple fixed point theorem.

Theorem: (Lawvere) If $e : A \to B^A$ is a surjection then every $f : B \to B$ has a fixed point.

Proof. Because $e$ is a surjection, there is $a \in A$ such that $e(a) = \lambda x : A \,.\, f(e(x)(x))$, but then $e(a)(a) = f(e(a)(a)$. $\Box$

Lawvere's original version is a bit more general, but the one given here makes is very clear that Lawvere's fixed point theorem is the diagonal argument in crystallized form. Indeed, the contrapositive form of the theorem, namely

Corollary: If $f : B \to B$ has no fixed point then there is no surjection $e : A \to B^A$.

immediately implies a number of famous theorems that rely on the diagonal argument. For example, there can be no surjection $A \to \lbrace 0, 1\rbrace^A$ because the map $x \mapsto 1 - x$ has no fixed point in $\lbrace 0, 1\rbrace$ -- and that is Cantors' theorem.

It not easy to find non-trivial instances to which Lawvere's theorem applies. Indeed, if excluded middle holds, then having a surjection $e : A \to B^A$ implies that $B$ is the singleton. We should look for interesting instances in categories other than classical sets. In my paper I do so: I show that countably based $\omega$-cpos in the effective topos are countable and closed under countable products, which gives us a rich supply of objects $B$ such that there is a surjection $\mathbb{N} \to B^\mathbb{N}$.

Enjoy the paper!

→ continue reading

It has been almost a decade since Matija Pretnar and I posted the first blog posts about programming with algebraic effects and handlers and the programming language Eff. Since then handlers have become a well-known control mechanism in programming languages.

Handlers and monads excel at simulating effects, either in terms of other effects or as pure computations. For example, the familiar state monad implements mutable state with (pure) state-passing functions, and there are many more examples. But I have always felt that handlers and monads are not very good at explaining how a program interacts with its external environment and how it gets to perform real-world effects.

Danel Ahman and I have worked for a while on attacking the question on how to better model external resources and what programming constructs are appropriate for working with them. The time is right for us to show what we have done so far. The theoretical side of things is explained in our paper Runners in action, Danel implemented a Haskell library Haskell-Coop to go with the paper, and I implemented a programming language Coop.

→ continue reading (5 comments)

Joel Hamkins advertised the following theorem on Twitter:

Theorem: All complete ordered fields are isomorphic.

The standard proof posted by Joel has two parts:

1. A complete ordered field is archimedean.
2. Using the fact that the rationals are dense in an archimedean field, we construct an isomorphism between any two complete ordered fields.

The second step is constructive, but the first one is proved using excluded middle, as follows. Suppose $F$ is a complete ordered field. If $b \in F$ is an upper bound for the natural numbers, construed as a subset of $F$, then so $b - 1$, but then no element of $F$ can be the least upper bound of $\mathbb{N}$. By excluded middle, above every $x \in F$ there is $n \in \mathbb{N}$.

So I asked myself and the constructive news mailing list what the constructive status of the theorem is. But something was amiss, as Fred Richman immediately asked me to provide an example of a complete ordered field. Why would he do that, don't we have the MacNeille reals? After agreeing on definitions, Toby Bartels gave the answer, which I am taking the liberty to adapt a bit and present here. I am probably just reinventing the wheel, so if someone knows an original reference, please provide it in the comments.

The theorem holds constructively, but for a bizarre reason: if there exists a complete ordered field, then the law of excluded middle holds, and the standard proof is valid!

→ continue reading (11 comments)

Published as arXiv:1807.05923.

Abstract: This note recapitulates and expands the contents of a tutorial on the mathematical theory of algebraic effects and handlers which I gave at the Dagstuhl seminar 18172 "Algebraic effect handlers go mainstream". It is targeted roughly at the level of a doctoral student with some amount of mathematical training, or at anyone already familiar with algebraic effects and handlers as programming concepts who would like to know what they have to do with algebra. We draw an uninterrupted line of thought between algebra and computational effects. We begin on the mathematical side of things, by reviewing the classic notions of universal algebra: signatures, algebraic theories, and their models. We then generalize and adapt the theory so that it applies to computational effects. In the last step we replace traditional mathematical notation with one that is closer to programming languages.

→ continue reading (2 comments)

You may have noticed that lately I have had trouble with the blog. It was dying periodically because the backend database kept crashing. It was high time I moved away from Wordpress anyway, so I bit the bullet and ported the blog.

→ continue reading (4 comments)

I gave a keynote talk "Derivations as Computations" at ICFP 2019.

• Slides with speaker notes: derivations-as-computations-icfp-2019.pdf
• Demo file: demo-icfp2019.m31

→ continue reading

Here are the slides with speaker notes for the talk What is an explicit bijection which I gave at the 31st International Conference on Formal Power Series and Algebraic Combinatorics (FPSAC 2019). It was the "outsider" talk, where they invite someone to tell them something outside of their area.

So how does one sell homotopy type theory to people who are interested in combinatorics? That is a tough sell. I used my MathOverflow question "What is an explicit bijection?" to give a stand-up comedy introduction, after which I plunged into type theory. I am told I plunged a little too hard. For instance, people asked "why are we doing this" because I did not make it clear enough that we are trying to make a distinction between "abstractly exists" and "concretely constructed". Oh well, it's difficult to explain homotopy type theory in 50 minutes. Anyhow, I hope you can get something useful from the slides.

Download slides: what-is-an-explicit-bijection.pdf

Video recording of the lecture is now available.

→ continue reading (2 comments)

This semester my colleague Jaka Smrekar and I are teaching a graduate course on homotopy theory and homotopy type theory. The first part was taught by Jaka and was a nice review of classical homotopy theory leading up to Quillen model categories. In the second part I am covering basic homotopy type theory.

The course materials are available at the GitHub repository homotopy-type-theory-course. The homotopy type theory lectures are also recorded on video.

→ continue reading (3 comments)

I was purging the disk on my laptop of large files and found a video lecture which I forgot to publish. Here it is with some delay. I lectured on how to implement type theory at the School and Workshop on Univalent Mathematics in December 2017, at the University of Birmingham (UK).

You may visit the GitHub repository spartan-type-theory. There used to be a video, but I lost it.

→ continue reading (1 comment)

I have had the honor to lecture at the Oregon Programming Language Summer School 2018 on the topic of algebraic effects and handlers. The notes, materials and the lectures are available online:

• the GitHub repository with the course material
• the OPLSS lecture materials, including notes and video recordings of the lectures

I gave four lectures which started with the mathematics of algebraic theories, explained how they can be used to model computational effects, how we make a programming language out of them, and how to program with handlers.

→ continue reading (3 comments)

The slides from the talk “Spartan type theory”, given at the School and Workshop on Univalent Mathematics.

Download slides with speaker notes: Spartan Type Theory [PDF]

→ continue reading (7 comments)

Here are the slides for the talk I just gave at TYPES 2017 in Budapest. It is joint work with Philipp Haselwarter and Théo Winterhalter. The abstract for the talk is available online.

It describes a complete formalization of dependent type theory which allows you to turn various features of type theory on and off, and it proves several basic formal theorems.

GitHub repository: formal-type-theory
Slides: TYPES 2017  – A modular formalization of type theory in Coq [PDF]

→ continue reading (5 comments)

We are looking for two PhD students at the Faculty of Mathematics and Physics, University of Ljubljana. The programme starts in October 2017 and lasts three years. The positions will be fully funded (subject to approval by the funding agency). The candidates should have a Master's degree in mathematics or computer science. No knowledge of Slovene is required.

The first PhD student will be advised by dr. Andrej Bauer. The topic of research is foundations of type theory. The candidate should have interest in mathematical aspects of type theory, and familiarity with proof assistants is desirable.

The second PhD student will be advised by dr. Matija Pretnar. The topic of research is the theory of programming languages with a focus on computational effects. The candidate should have interest in both the mathematical foundations and practical implementation of programming languages.

Candidates should send their applications as soon as possible, but no later than the end of April, to Andrej Bauer or Matija Pretnar, depending on their primary interest. Please include a short CV, academic record, and a statement of interest.

→ continue reading

In 2013 I gave a talk about constructive mathematics “Five stages of accepting constructive mathematics” (video) at the Institute for Advanced Study. I turned the talk into a paper, polished it up a bit, added things here and there, and finally it has now been published in the Bulletin of the American Mathematical Society. It is not quite a survey paper, but it is not very technical either. I hope you will enjoy reading it.

Free access to the paper:  Five stages of accepting constructive mathematics (PDF)

→ continue reading (12 comments)

It is my pleasure to announce the new and improved Programming languages Zoo, a potpourri of miniature but fully functioning programming language implementations. The new zoo has a decent web site, it is now hosted on GitHub, and the source code was cleaned up. Many thanks to Matija Pretnar for all the work.

The purpose of the zoo is to demonstrate design and implementation techniques, from dirty practical details to lofty theoretical considerations:

• functional, declarative, object-oriented, and procedural languages
• source code parsing with a parser generator
• recording of source code positions
• pretty-printing of values
• interactive shell (REPL) and non-interactive file processing
• untyped, statically and dynamically typed languages
• type checking and type inference
• subtyping, parametric polymorphism, and other kinds of type systems
• eager and lazy evaluation strategies
• recursive definitions
• exceptions
• interpreters and compilers
• abstract machine

There is still a lot of room for improvement and new languages. Contributions are welcome!

 

→ continue reading

I have participated in a couple of lengthy discussions about formal proofs. I realized that an old misconception is creeping in. Let me expose it.

→ continue reading (24 comments)

Mike Shulman just wrote a very nice blog post on what is a formal proof. I much agree with what he says, but I would like to offer my own perspective. I started writing it as a comment to Mike's post and then realized that it is too long, and that I would like to have it recorded independently as well. Please read Mike's blog post first.

→ continue reading (55 comments)

This post is going to draw an angry Haskell mob, but I just have to say it out loud: I have never seen a definition of the so-called category Hask and I do not actually believe there is one until someone does some serious work.

→ continue reading (66 comments)

I am about to give an invited talk at the  Workshop on Categorical Logic and Univalent Foundations 2016 in Leeds, UK. It's a charming workshop that I am enjoing a great deal. Here are the slides of my talk, with speaker notes, as well as the Andromeda examples that I am planning to cover.

• Slides: AndromedaProofAssistant.pdf
  
• Andromeda files: nat.m31, universe.m31

→ continue reading (30 comments)

I am about to give an invited talk at the Computability and Complexity in Analysis 2016 conference (yes, I am in the south of Portugal, surrounded by loud English tourists, but we are working here, in a basement no less). Here are the slides, with extensive speaker notes, comment and questions are welcome.

Slides: hott-reals-cca2016.pdf

→ continue reading (6 comments)

In a paper accepted at POPL 2016 Matt Brown and Jens Palsberg constructed a self-interpreter for System $F_\omega$, a strongly normalizing typed $\lambda$-calculus. This came as a bit of a surprise as it is “common knowledge” that total programming languages do not have self-interpreters.

Thinking about what they did I realized that their conditions allow a self-interpreter for practically any total language expressive enough to encode numbers and pairs. In the PDF note accompanying this post I give such a self-interpreter for Gödel's System T, the weakest such calculus. It is clear from the construction that I abused the definition given by Brown and Palsberg. Their self-interpreter has good structural properties which mine obviously lacks. So what we really need is a better definition of self-interpreters, one that captures the desired structural properties. Frank Pfenning and Peter Lee called such properties reflexivity, but only at an informal level. Can someone suggest a good definition?

Note: self-interpreter-for-T.pdf

→ continue reading (11 comments)

A postdoc position in the Effmath research project is available at the University of Ljubljana, Faculty of Mathematics and Physics. The precise topic is flexible, but should generally be aligned with the project (see project description). Possible topics include:

•  reasoning about computational effects
•  implementation of computational effects
• proof assistants and formalization of mathematics

The candidate should have a PhD degree in mathematics or computer science, with background knowledge relevant to the project area. The position is available for a period of one year with possibility of extension, preferably starting in early 2016. No knowledge of the Slovene language is required.

The candidates should contact Andrej Bauer by email as soon as possible, but no later than January 8th 2016. Please include a short CV and a statement of interest.

→ continue reading

My student Marko Koležnik is about to finish his Master's degree in Mathematics at the University of Ljubljana. He implemented Agda Writer, a graphical user interface  for the Agda proof assistant on the OS X platform. As he puts it, the main advantage of Agda Writer is no Emacs, but the list of cool features is a bit longer:

• bundled Agda: it comes with preinstalled Agda so there is zero installation effort (of course, you can use your own Agda as well).
• UTF-8 keyboard shortcuts: it is super-easy to enter UTF-8 characters by typing their LaTeX names, just like in Emacs. It trumps Emacs by converting ASCII arrows to their UTF8 equivalents on the fly. In the preferences you can customize the long list of shortcuts to your liking.
• the usual features expected on OS X are all there: auto-completion, clickable error messages and goals, etc.

Agda Writer is open source. Everybody is welcome to help out and participate on the Agda Writer repository.

Who is Agda Writer for? Obviously for students, mathematicians, and other potential users who were not born with Emacs hard-wired into their brains. It is great for teaching Agda as you do not have to spend two weeks explaining Emacs. The only drawback is that it is limited to OS X. Someone should write equivalent Windows and Linux applications. Then perhaps proof assistants will have a chance of being more widely adopted.

→ continue reading (5 comments)

This is officially a rant and should be read as such.

Here is my pet peeve: theoretical computer scientists misuse the word “provably”. Stop it. Stop it!

→ continue reading (10 comments)

I have not written a blog post in a while, so I decided to write up a short observation about truth values in intuitionistic logic which sometimes seems a bit puzzling.

Let $\Omega$ be the set of truth values (in Coq this would be the setoid whose underlying type is $\mathsf{Prop}$ and equality is equivalence $\leftrightarrow$, while in HoTT it is the h-propostions). Call a truth value $p : \Omega$ intermediate if it is neither true nor false, i.e., $p \neq \bot$ and $p \neq \top$. Such a “third” truth value $p$ is proscribed by excluded middle.

The puzzle is to explain how the following two facts fit together:

1. “There is no intermediate truth value” is an intuitionistic theorem.
2. There are models of intuitionistic logic with many truth values.

→ continue reading (6 comments)

Here are the slides of my TYPES 2015 talk “The troublesome reflection rule” with fairly detailed presenter notes. The meeting is  taking place in Tallinn, Estonia – a very cool country in many senses (it's not quite spring yet even though we're in the second half of May, and it's the country that gave us Skype).

Download slides: The troublesome reflection rule (TYPES 2015) [PDF].

→ continue reading (2 comments)

It is my pleasure to announce a second PhD position in Ljubljana!

A position is available for a PhD student at the University of Ljubljana in the general research area of modelling and reasoning about computational effects. The precise topic is somewhat flexible, and will be decided in discussion with the student. The PhD will be supervised by Alex Simpson who is Professor of Computer Science at the Faculty of Mathematics and Physics.

The position will be funded by the Effmath project (see project description). Full tuition & stipend will be provided.

The candidate should have a master's (or equivalent) degree in either mathematics or computer science, with background knowledge relevant to the project area. The student will officially enrol in October 2015 at the University of Ljubljana. No knowledge of the Slovene language is required.

The candidates should contact Alex.Simpson@fmf.uni-lj.si by email as soon as possible. Please include a short CV and a statement of interest.

→ continue reading

I am looking for a PhD student in mathematics. Full tuition & stipend will be provided for a period of three years, which is also the official length of the programme. The topic of research is somewhat flexible and varies from constructive models of homotopy type theory to development of a programming language for a proof assistant based on dependent type theory, see the short summary of the Effmath project for a more detailed description.

The candidate should have as many of the following desiderata as possible, and at the very least a master's degree (or an equivalent one):

1. a master's degree in mathematics, with good knowledge of computer science
2. a master's degree in computer science, with good knowledge of mathematics
3. experience with functional programming
4. experience with proof assistants
5. familiarity with homotopy type theory

The student will officially enrol in October 2015 at the University of Ljubljana. No knowledge of Slovene is required. However, it is possible, and even desirable, to start with the actual work (and stipend) earlier, as soon as in the spring of 2015. The candidates should contact me by email as soon as possible. Please include a short CV and a statement of interest.

Update 2015-03-28: the position has been taken.

→ continue reading

I spoke at TEDx University of Ljubljana. The topic was how programming influences various aspects of life. I showed the audence how a bit of simple programming can reveal the beauty of mathematics. Taking John Baez's The Bauty of Roots as an inspiration, I drew a very large image (20000 by 17500 pixels) of all roots of all polynomials of degree at most 26 whose coefficients are $-1$ or $1$. That's 268.435.452 polynomials and 6.979.321.752 roots. It is two degrees more than Sam Derbyshire's image,  so consider the race to be on! Who can give me 30 degrees?

→ continue reading (7 comments)

Here are the slides from my Logic Coloquium 2014 talk in Vienna. This is joint work with Kazuto Yoshimura from Japan Advanced Institute for Science and Technology.

Abstract: In constructive mathematics we often consider implications between non-constructive reasoning principles. For instance, it is well known that the Limited principle of omniscience implies that equality of real numbers is decidable. Most such reductions proceed by reducing an instance of the consequent to an instance of the antecedent. We may therefore define a notion of instance reducibility, which turns out to have a very rich structure. Even better, under Kleene's function realizability interpretation instance reducibility corresponds to Weihrauch reducibility, while Kleene's number realizability relates it to truth-table reducibility. We may also ask about a constructive treatment of other reducibilities in computability theory. I shall discuss how one can tackle Turing reducibility constructively via Kleene's number realizability.

Slides with talk notes:  lc2014-slides-notes.pdf

→ continue reading

In the post Seemingly impossible functional programs, I wrote increasingly efficient Haskell programs to realize the mathematical statement

$\forall p : X \to 2. (\exists x:X.p(x)=0) \vee (\forall x:X.p(x)=1)$

for $X=2^\mathbb{N}$, the Cantor set of infinite binary sequences, where $2$ is the set of binary digits. Then in the post A Haskell monad for infinite search in finite time I looked at ways of systematically constructing such sets $X$ with corresponding Haskell realizers of the above omniscience principle.

In this post I give examples of infinite sets $X$ and corresponding constructive proofs of their omniscience that are intended to be valid in Bishop mathematics, and which I have formalized in Martin-Löf type theory in Agda notation. This rules out the example $X=2^\mathbb{N}$, as discussed below, but includes many interesting infinite examples. I also look at ways of constructing new omniscient sets from given ones. Such sets include, in particular, ordinals, for which we can find minimal witnesses if any witness exists.

Agda is a dependently typed functional programming language based on Martin-Löf type theory. By the Curry-Howard correspondence, Agda is also a language for formulating mathematical theorems (types) and writing down their proofs (programs). Agda acts as a thorough referee, only accepting correct theorems and proofs. Moreover, Agda can run your proofs. Here is a graph of the main Agda modules for this post, and here is a full graph with all modules.

→ continue reading (1 comment)

I just gave a talk at “Semantics of proofs and certified mathematics”. I spoke about a new proof checker Chris Stone and I are working on. The interesting feature is that it has both kinds of equality, the “paths” and the “strict” ones. It is based on a homotopy type system proposed by Vladimir Voevodsky. The slides contain talk notes and explain why it is “Brazilian”.

Download slides: brazilian-type-checking.pdf

GitHub repository: https://github.com/andrejbauer/tt

Abstract: Proof assistants verify that inputs are correct up to judgmental equality. Proofs are easier and smaller if equalities without computational content are verified by an oracle, because proof terms for these equations can be omitted. In order to keep judgmental equality decidable, though, typical proof assistants use a limited definition implemented by a fixed equivalence algorithm. While other equalities can be expressed using propositional identity types and explicit equality proofs and coercions, in some situations these create prohibitive levels of overhead in the proof.
Voevodsky has proposed a type theory with two identity types, one propositional and one judgmental. This lets us hypothesize new judgmental equalities for use during type checking, but generally renders the equational theory undecidable without help from the user.

Rather than reimpose the full overhead of term-level coercions for judgmental equality, we propose algebraic effect handlers as a general mechanism to provide local extensions to the proof assistant's algorithms. As a special case, we retain a simple form of handlers even in the final proof terms, small proof-specific hints that extend the trusted verifier in sound ways.

→ continue reading (5 comments)

This is a draft version of my contribution to “A Computable Universe: Understanding and Exploring Nature as Computation”, edited by Hector Zenil. Consider it a teaser for the rest of the book, which contains papers by an impressive list of authors.

Abstract: Intuitionistic mathematics perceives subtle variations in meaning where classical mathematics asserts equivalence, and permits geometrically and computationally motivated axioms that classical mathematics prohibits. It is therefore well-suited as a logical foundation on which questions about computability in the real world are studied. The realizability interpretation explains the computational content of intuitionistic mathematics, and relates it to classical models of computation, as well as to more speculative ones that push the laws of physics to their limits. Through the realizability interpretation Brouwerian continuity principles and Markovian computability axioms become statements about the computational nature of the physical world.

Download: real-world-realizability.pdf

→ continue reading (5 comments)

A discussion on the homotopytypetheory mailing list prompted me to write this short note. Apparently a mistaken belief has gone viral among certain mathematicians that Univalent foundations is somehow limited to constructive mathematics. This is false. Let me be perfectly clear:

Univalent foundations subsume classical mathematics!

The next time you hear someone having doubts about this point, please refer them to this post. A more detailed explanation follows.

→ continue reading (24 comments)

A student of mine worked on a project to produce beautiful pictures of Costa's minimal surface with the PovRay ray tracer. For this purpose she needed to triangulate the and compute normals to it at the vertices. It is not too hard to do the latter part, and the Internet offers several ways of doing it, but the normals are a bit tricky. If anyone can calculate them with paper and pencil I'd like to hear about it.

I went back to my undergraduate days when I actually did differential geometry and churned out the normals with Mathematica. It took a bit of work, kind advice from my colleague Pavle Saksida, and a pinch of black magic (to extract the Delaunay triangulation from Mathematica), so I thought I might as well publish the result at my GitHub costa-surface repository. The code is released into public domain. Have fun making pictures of Costa's surface! Here is mine (deliberately non-fancy):

→ continue reading

In the HoTT book issue 460 a question by gluttonousGrandma (where do people get these nicknames?) once more exposed a common misunderstanding that we tried to explain in section 5.8 of the book (many thanks to Bas Spitters for putting the book into Google Books so now we can link to particular pages). Apparently the following belief is widely spread, and I admit to holding it a couple of years ago:

An inductive type contains exactly those elements that we obtain by repeatedly using the constructors.

If you believe the above statement you should keep reading. I am going to convince you that the statement is unfounded, or that at the very least it is preventing you from understanding type theory.

→ continue reading (29 comments)

Recently I reviewed a paper in which most proofs were done in a proof assistant. Yes, the machine guaranteed that the proofs were correct, but I still had to make sure that the authors correctly formulated their definitions and theorems, that the code did not contain hidden assumptions, that there were no unfinished proofs, and so on.

In a typical situation an author submits a paper accompanied with some source code which contains the formalized parts of the work. Sometimes the code is enclosed with the paper, and sometimes it is available for download somewhere. It is easy to ignore the code! The journal finds it difficult to archive the code, the editor naturally focuses on the paper itself, the reviewer trusts the authors and the proof assistant, and the authors are tempted not to mention dirty little secrets about their code. If the proponents of formalized mathematics want to avert a disaster that could destroy their efforts in a single blow, they must adopt a set of rules that will ensure high standards. There is much more to trusting a piece of formalized mathematics than just running it through a proof checker.

→ continue reading (17 comments)

The HoTT book is finished!

Since spring, and even before that, I have participated in a great collaborative effort on writing a book on Homotopy Type Theory. It is finally finished and ready for public consumption. You can get the book freely at http://homotopytypetheory.org/book/. Mike Shulman has written about the contents of the book, so I am not going to repeat that here. Instead, I would like to comment on the socio-technological aspects of making the book, and in particular about what we learned from open-source community about collaborative research.

→ continue reading (10 comments)

Mathematicians are often confused about the meaning of variables. I hear them say “a free variable is implicitly universally quantified”, by which they mean that it is ok to equate a formula $\phi$ with a free variable $x$ with its universal closure $\forall x \,.\, \phi$. I am addressing this post to those who share this opinion.

→ continue reading (31 comments)

I spent a week trying to implement higher-order pattern unification. I looked at couple of PhD dissertations, talked to lots of smart people, and failed because the substitutions were just getting in the way all the time. So today we are going to bite the bullet and implement de Bruijn indices and explicit substitutions.

The code is available on Github in the repository andrejbauer/tt (the blog-part-III branch).

→ continue reading (6 comments)

I am on a roll. In the second post on how to implement dependent type theory we are going to:

1. Spiff up the syntax by allowing more flexible syntax for bindings in functions and products.
2. Keep track of source code locations so that we can report where the error has occurred.
3. Perform normalization by evaluation.

→ continue reading (9 comments)

I am spending a semester at the Institute for Advanced Study where we have a special year on Univalent foundations. We are doing all sorts of things, among others experimenting with type theories. We have got some real experts here who know type theory and Coq inside out, and much more, and they're doing crazy things to Coq (I will report on them when they are done). In the meanwhile I have been thinking how one might implement dependent type theories with undecidable type checking. This is a tricky subject and I am certainly not the first one to think about it. Anyhow, if I want to experiment with type theories, I need a small prototype first. Today I will present a very minimal one, and build on it in future posts.

Make a guess, how many lines of code does it take to implement a dependent type theory with universes, dependent products, a parser, lexer, pretty-printer, and a toplevel which uses line-editing when available?

→ continue reading (9 comments)

It seems to me that people think I am a constructive mathematician, or worse a constructivist (a word which carries a certain amount of philosophical stigma). Let me be perfectly clear: it is not decidable whether I am a constructive mathematician.

→ continue reading (44 comments)

I am sitting on a tutorial on categorical semantics of dependent type theory given by Peter Lumsdaine. He is talking about categories with attributes and other variants of categories that come up in the semantics of dependent type theory. He is amazingly good at fielding questions about definitional equality from the type theorists. And it looks like some people are puzzling over pullbacks showing up, which Peter is about to explain using syntactic categories. Here is a pedestrian explanation of a very important fact:

Substitution is pullback.

→ continue reading (14 comments)

Egbert Rijke successfully defended his master thesis in Utrecht a couple of weeks ago. He published it on the Homotopy type theory blog (here is a direct link to the PDF file (revised)). The thesis is well written and it contains several new results, but most importantly, it is a gentle yet non-trivial introduction to homotopy type theory. If you are interested in the topic but do not know where to start, Egbert's thesis might be perfect for you. As far as I know it is the first substantial piece of text written in (informal) homotopy type theory.

What I find most amazing about the work is that Egbert does not have to pretend to be a homotopy type theorist, like us old folks. His first contact with type theory was homotopy type theory, which impressed on his mind a new kind of geometric intuition about $\Pi$'s, $\Sigma$'s and $\mathrm{Id}$'s. If we perform enough such experiments on young bright students, strange things will happen.

→ continue reading (4 comments)

This is an advertisement for two great meetings we are organizing in Ljubljana from June 15 to June 20, 2012:

• Fourth workshop on formal topology (June 15—19)
• Workshop on Higher Dimensional Algebra, Categories and Types (June 20)

There are many reasons why you should come: Ljubljana is lovely in June, with many cafes and restaurants on the Ljubljanica river bank, we have a very interesting programme, and when will you next be able to attend a meeting in which the keynote speakers are Per Martin-Löf, Ieke Moerdijk and Vladimir Voevodsky? Not to mention that the schedule is fairly light, everything is within walking distance, and we are organizing dinners at some excellent restaurants.

If you decide to come, make sure to book a hotel early and register today!

→ continue reading (4 comments)

I remember how hard it was to assimilate category theory when I was a student. A beginning student on math.stackexchange.com is asking for a solution to a basic lemma about pullbacks. It really is the sort of thing one should do by oneself. Nevertheless, here it is, in gory details.

Download: pullback.pdf

→ continue reading (1 comment)

It is well known that, both in constructive mathematics and in programming languages, types are secretly topological spaces and functions are secretly continuous. I have previously exploited this in the posts Seemingly impossible functional programs and A Haskell monad for infinite search in finite time, using the language Haskell. In languages based on Martin-Löf type theory such as Agda, there is a set of all types. This can be used to define functions $\mathbb{N} \to \mathrm{Set}$ that map numbers to types, functions $\mathrm{Set} \to \mathrm{Set}$ that map types to types, and so on.

Because $\mathrm{Set}$ itself is a type, a large type of small types, it must have a secret topology. What is it? There are a number of ways of approaching topology. The most popular one is via open sets. For some spaces, one can instead use convergent sequences, and this approach is more convenient in our situation. It turns out that the topology of the universe $\mathrm{Set}$ is indiscrete: every sequence of types converges to any type! I apply this to deduce that $\mathrm{Set}$ satisfies the conclusion of Rice's Theorem: it has no non-trivial, extensional, decidable property.

To see how this works, check:

• A short paper with the proofs in mathematical vernacular, and further discussion of the intuitions, motivations and consequences.
• Literate proofs in Agda of the universe indiscreteness theorem and Rice's Theorem for the universe.
• Agda proofs of related facts.

The Agda pages can be navigated be clicking at any (defined) symbol or word, in particular by clicking at the imported module names.

→ continue reading (2 comments)

Matija and I are pleased to announce a new major release of the eff programming language.

In the last year or so eff has matured considerably:

• It now looks and feels like OCaml, so you won't have to learn yet another syntax.
• It has static typing with parametric polymorphism and type inference.
• Eff now clearly separates three basic concepts: effect types, effect instances, and handlers.
• How eff works is explained in our paper on Programming with Algebraic Effects and Handlers.
• We moved the source code to GitHub, so go ahead and fork it!

→ continue reading (6 comments)

With Matija Pretnar.

Abstract: Eff is a programming language based on the algebraic approach to computational effects, in which effects are viewed as algebraic operations and effect handlers as homomorphisms from free algebras. Eff supports first-class effects and handlers through which we may easily define new computational effects, seamlessly combine existing ones, and handle them in novel ways. We give a denotational semantics of eff and discuss a prototype implementation based on it. Through examples we demonstrate how the standard effects are treated in eff, and how eff supports programming techniques that use various forms of delimited continuations, such as backtracking, breadth-first search, selection functionals, cooperative multi-threading, and others.

Download paper: eff.pdf

ArXiv version: arXiv:1203.1539v1 [cs.PL]

To read more about eff, visit the eff page.

→ continue reading (19 comments)

While making a comment on Stackoverflow I noticed something: suppose we have a term in the $\lambda$-calculus in which no abstracted variable is used more than once. For example, $\lambda a b c . (a b) (\lambda d. d c)$ is such a term, but $\lambda f . f (\lambda x . x x)$ is not because $x$ is used twice. If I am not mistaken, all such terms can be typed. For example:

# fun a b c -> (a b) (fun d -> d c) ;;
- : ('a -> (('b -> 'c) -> 'c) -> 'd) -> 'a -> 'b -> 'd = 

# fun a b c d e e' f g h i j k l m n o o' o'' o''' p q r r' s t u u' v w x y z ->
    q u i c k b r o w n f o' x j u' m p s o'' v e r' t h e' l a z y d o''' g;;
  - : 'a -> 'b -> 'c -> 'd -> 'e -> 'f -> 'g -> 'h -> 'i -> 'j ->
    'k -> 'l -> 'm -> 'n -> 'o -> 'p -> 'q -> 'r -> 's -> 't ->
    ('u -> 'j -> 'c -> 'l -> 'b -> 'v -> 'p -> 'w -> 'o -> 'g ->
     'q -> 'x -> 'k -> 'y -> 'n -> 't -> 'z -> 'r -> 'a1 -> 'e ->
     'b1 -> 'c1 -> 'i -> 'f -> 'm -> 'a -> 'd1 -> 'e1 -> 'd -> 's
     -> 'h -> 'f1) -> 'v -> 'b1 -> 'z -> 'c1 -> 'u -> 'y -> 'a1
     -> 'w -> 'x -> 'e1 -> 'd1 -> 'f1 = 
</pre>

What is the easiest way to see that this really is the case?

A related question is this (I am sure people have thought about it): how big can a type of a typeable $\lambda$-term be? For example, the Ackermann function can be typed as follows, although the type prevents it from doing the right thing in a typed setting:

# let one = fun f x -> f x ;;
val one : ('a -> 'b) -> 'a -> 'b =
# let suc = fun n f x -> n f (f x) ;;
val suc : (('a -> 'b) -> 'b -> 'c) -> ('a -> 'b) -> 'a -> 'c =
# let ack = fun m -> m (fun f n -> n f (f one)) suc ;;
val ack :
  ((((('a -> 'b) -> 'a -> 'b) -> 'c) ->
   (((('a -> 'b) -> 'a -> 'b) -> 'c) -> 'c -> 'd) -> 'd) ->
   ((('e -> 'f) -> 'f -> 'g) -> ('e -> 'f) -> 'e -> 'g) -> 'h) -> 'h = 
</pre>

That's one mean type there! Can it be “explained”? Hmm, why _does_ `ack` compute the Ackermann function in the untyped $\lambda$-calculus?

→ continue reading (5 comments)

With Peter LeFanu Lumsdaine.

Abstract: The Bourbaki-Witt principle states that any progressive map on a chain-complete poset has a fixed point above every point. It is provable classically, but not intuitionistically. We study this and related principles in an intuitionistic setting. Among other things, we show that Bourbaki-Witt fails exactly when the trichotomous ordinals form a set, but does not imply that fixed points can always be found by transfinite iteration. Meanwhile, on the side of models, we see that the principle fails in realisability toposes, and does not hold in the free topos, but does hold in all cocomplete toposes.

Download paper: bw.pdf
ArXiv version: arXiv:1201.0340v1 [math.CT]

This paper is an extension of my previous paper on the Bourbaki-Witt and Knaster-Tarski fixed-point theorems in the effective topos (arXiv:0911.0068v1).

→ continue reading

On December 6th 2011 I gave a talk about homotopy equivalences in the context of homotopy type theory at our seminar for foundations of mathematics and theoretical computer science. I discuss the differences and relations between isomorphism (in the sense of type theory), an adjoint equivalence, and a homotopy equivalence. Even though the talk itself was not super-well prepared, I hope the recording will be interesting to some people. I was going fairly slowly, so it should be possible to follow the talk. I apologize for such a long video, but I really did not see how to chop it up into smaller pieces. Also, I need to figure out why I cannot fast forward the video beyond what has been downloaded.

Video recording: HoTT Equivalences

→ continue reading (5 comments)

A talk given at “Mathematics, Algorithms and Proofs 2011” at the Lorentz Center in Leiden, the Netherlands. I explain how to use computational effects to speed up Martin Escardo's impossible functionals.

Video recording: How to make the ‘impossible’ functionals run even faster

→ continue reading (4 comments)

A talk given at “Computation with Infinite Data: Logical and Topological Foundations” Dagstuhl seminar 11411. I describe a realizability model based on infinite-time Turing machines in which it is possible to embed the Baire space (infinite sequences of numbers) into the space of numbers.

Also see the post Constructive gem: an injection from Baire space to natural numbers for written notes on this topic.

Video recording: Embedding the Baire space into natural numbers

→ continue reading

Last year I participated in a project whose goal was to record at low cost my lectures on video and put them on-line. Since the most expensive parts of recording are having a camera man and manual post production, we set up a static camera and just uploaded raw video online at videolectures.net. As you can see for yourself, the sound is good (I wore a microphone) but the whiteboard is mostly illegible. In addition, it took about two weeks for the lectures to show up on-line because there were men-in-the-middle. So that got me thinking whether there was a better way.

→ continue reading (23 comments)

In an earlier post I talked about the modulus of continuity functional, where I stated that it cannot be defined without using some form of computational effects. It is a bit hard to find the proof of this fact so I am posting it on my blog in two parts, for Google and everyone else to find more easily. In the first part I show that there is no extensional modulus of continuity. In the second part I will show that every functional that is defined in PCF (simply-typed $\lambda$-calculus with natural numbers and recursion) is extensional. 

→ continue reading (8 comments)

I am not sure whether to call this one a constructive gem or stone. I suppose it is a matter of personal taste. I think it is a gem, albeit a very unusual one: there is a topos in which $\mathbb{N}^\mathbb{N}$ can be embedded into $\mathbb{N}$.

→ continue reading (3 comments)

With Karin Cvetko Vah.

For the last two months or so I got “distracted” by a topic which is not properly my core interest, namely non-commutative algebra. It was very strange at first, but now that I got used to non-commutative lattices (yes, there is such a thing) it's kind of fun. Anyhow, Karin Cvetko Vah and I worked out Stone duality for skew Boolean algebras with intersections. Classical Stone duality tells us that Boolean algebras are dual to Stone spaces (zero-dimensional compact Hausdorff spaces), and that the generalized Boolean algebras (which are like Boolean algebras without a top element) are dual to Boolean spaces (zero-dimensional locally-compact Hausdorff spaces). Our skew version of duality says that right-handed skew Boolean algebras with intersections are dual to surjective etale maps between Boolean spaces. It is quite a mouthful to say “right-handed skew Boolean algebra with intersections”, let alone get used to it, but in a certain sense this is a very natural non-commutative structure. And we can get rid of the “right-handed” condition to obtain duality for “skew Boolean algebras with intersections”, as well as several other versions. We use the duality to construct a right-handed skew Boolean algebra with intersections which does not have a lattice section. It has been an open question whether such skew lattices exist.

Download: sba.pdf

arXiv: 1106.0425

Abstract: We extend Stone duality between generalized Boolean algebras and Boolean spaces, which are the zero-dimensional locally-compact Hausdorff spaces, to a non-commutative setting. We first show that the category of right-handed skew Boolean algebras with intersections is dual to the category of surjective étale maps between Boolean spaces. We then extend the duality to skew Boolean algebras with intersections, and consider several variations in which the morphisms are restricted. Finally, we use the duality to construct a right-handed skew Boolean algebra without a lattice section.

And now I can get back to homotopy type theory and Coq hacking.

→ continue reading (1 comment)

As a preparation for my part of a joint tutorial Programs from proofs at MFPS 27 at the end of this month with Ulrich Berger, Monika Seisenberger, and Paulo Oliva, I've developed in Agda some things we've been doing together.

Using

• Berardi-Bezem-Coquand functional, or alternatively,
• Berger-Oliva modified bar recursion, or alternatively,
• Escardo-Oliva countable product of selection functions,

for giving a proof term for classical countable choice, we prove the classical infinite pigeonhole principle in Agda: every infinite boolean sequence has a constant infinite subsequence, where the existential quantification is classical (double negated).

As a corollary, we get the finite pigeonhole principle, using Friedman's trick to make the existential quantifiers intuitionistic.

This we can run, and it runs fast enough. The point is to illustrate in Agda how we can get witnesses from classical proofs that use countable choice. The finite pigeonhole principle has a simple constructive proof, of course, and hence this is really for illustration only.

The main Agda files are

• InfinitePigeon
• FinitePigeon
• Examples

These are Agda files converted to html so that you can navigate them by clicking at words to go to their definitions. A zip file with all Agda files is available. Not much more information is available here.

The three little modules that implement the Berardi-Bezem-Coquand, Berger-Oliva and Escardo-Oliva functionals disable the termination checker, but no other module does. The type of these functionals in Agda is the J-shift principle, which generalizes the double-negation shift.

→ continue reading (3 comments)

Bob Harper of CMU, has recently started a blog, called Existential Type, about programming languages. He is a leading expert in Programming Languages. I remember being deeply inspired the first time I heard him talk. I was an incoming graduate student at CMU and he presented what the programming languages people at CMU did. His posts are fun to read, unreserved and very educational. Highly recommended!

→ continue reading

Next week I am going to a meeting where I am supposed to give a tutorial on the Coq proof assistant. Inspired by the Catsters, I decided to prepare the material in the form of screencasts. You can find the first few tutorials on Youtube in my “Coq tutorials” playlist. So far I have:

• Obtaining and installing the Coq proof assistant
• How to use CoqIDE
• How to use Coq with Proof General
• A first proof with Coq (Frobenius rule)
• The dual Frobenius rule, part 1
• The dual Frobenius rule, part 2
• Currying and uncurrying, part 1
• Currying and uncurrying, part 2

You should turn on the high quality HD stream when you watch these. Feedback is welcome (and easy to provide on Youtube). I find it very, very difficult to listen to my own voice. I hope to have many more lectures soon, but I am starting to feel out of my depth, so if anyone wants to help they are welcome!

→ continue reading (17 comments)

Jens Blanck and I presented a paper at Computability and Complexity in Analysis 2009 with a complicated title (I like complicated titles):

Canonical Effective Subalgebras of Classical Algebras as Constructive Metric Completions

which has been published in Volume 16, Issue 18 of the Journal of Universal Computer Science. I usually just post the abstract, but this time I would like to explain the general idea informally, the way one can do it on a blog. But first, here is the abstract:

Abstract: We prove general theorems about unique existence of effective subalgebras of classical algebras. The theorems are consequences of standard facts about completions of metric spaces within the framework of constructive mathematics, suitably interpreted in realizability models. We work with general realizability models rather than with a particular model of computation. Consequently, all the results are applicable in various established schools of computability, such as type 1 and type 2 effectivity, domain representations, equilogical spaces, and others.

Download paper: effalg.pdf or directly from JUCS

→ continue reading (1 comment)

Alg is a program for enumeration of finite models of single-sorted first-order theories. These include groups, rings, fields, lattices, posets, graphs, and many more. Alg was written as a class project by Aleš Bizjak, a student of mine whose existence I cannot confirm with a URL. I joined the effort, added bells and whistles, as well as an alternative algorithm that works well for relational structures. Alg is ready for public consumption, although it should be considered of “beta” quality. Instructions for downloading alg are included at the end of this post.

→ continue reading (5 comments)

Alex Simpson, Matija Pretnar and I are organizing a workshop on computational effects. It will take place in Ljubljana on March 17th and 18th 2011. More information is available at the workshop web page.

→ continue reading

I think I am getting addicted to Coq, or more generally to doing mathematics, including the proofs, with computers. I spent last week finalizing a formalization of Gödel's functional interpretation of logic, also known as the Dialectica interpretation. There does not seem to be one available already, which is a good opportunity for a blog post.

→ continue reading (6 comments)

[Edit 2010-11-12: Given the gap in my “proof”, I am changing the title of the post to a question.]

I would like to record the following fact, which is hard to find on the internet: every subgroup is an equalizer, constructively. In other words, all monos in the category of groups are regular, constructively. It is interesting that this fact fails if we work in a meta-theory with “poor quotients”.

→ continue reading (9 comments)

[UPDATE 2012-03-08: since this post was written eff has changed considerably. For updated information, please visit the eff page.]

**Let's keep the blog rolling! Here are delimited continuations in eff, and a bunch of questions I do not know the answers to.

→ continue reading (6 comments)

[UPDATE 2012-03-08: since this post was written eff has changed considerably. For updated information, please visit the eff page.]

From some of the responses we have been getting it looks like people think that the io effect in eff is like unsafePerformIO in Haskell, namely that it causes an effect but pretends to be pure. This is not the case. Let me explain how eff handles built-in effects.

→ continue reading

[UPDATE 2012-03-08: since this post was written eff has changed considerably. For updated information, please visit the eff page.]

**This is a second post about the programming language eff. We covered the theory behind it in a previous post. Now we turn to the programming language itself.

Please bear in mind that eff is an academic experiment. It is not meant to take over the world. Yet. We just wanted to show that the theoretical ideas about the algebraic nature of computational effects can be put into practice. Eff has many superficial similarities with Haskell. This is no surprise because there is a precise connection between algebras and monads. The main advantage of eff over Haskell is supposed to be the ease with which computational effects can be combined.

→ continue reading (7 comments)

[UPDATE 2012-03-08: since this post was written eff has changed considerably. For updated information, please visit the eff page.]

I just returned from Paris where I was visiting the INRIA ?r² team. It was a great visit, everyone was very hospitable, the food was great, and the weather was nice. I spoke at their seminar where I presented a new programming language eff which is based on the idea that computational effects are algebras. The language has been designed and implemented jointly by Matija Pretnar and myself. Eff is far from being finished, but I think it is ready to be shown to the world. What follows is an extended transcript of the talk I gave in Paris. It is divided into two posts. The present one reviews the basic theory of algebras for a signature and how they are related to computational effects. The impatient readers can skip ahead to the second part, which is about the programming language.

A side remark: I have updated the blog to WordPress to 3.0 and switched to MathJax for displaying mathematics. Now I need to go through 70 old posts and convert the old ASCIIMathML notation to MathJax, as well as fix characters which got garbled during the update. Oh well, it is an investment for the future.

→ continue reading (18 comments)

Since the death of my old web server my Random Art has not worked. Bringing it up to date and installing it on the new server was a nightmare in software management. But it was worth it. The new Random Art runs the random art program inside your browser!

→ continue reading (14 comments)

Martin Escardo and Paulo Oliva have been working on the selection monad and related functionals. The selection monad `S(X) = (X -> R) -> X` is a cousin of the continuation monad `C(X) = (X -> R) -> R` and it has a lot of useful and surprising applications. I recommend their recent paper “What Sequential Games, the Tychonoff Theorem and the Double-Negation Shift have in Common” which they wrote for MSFP 2010 (if you visit the workshop you get to hear Martin live). They explain things via examples written in Haskell, starting off with the innocently looking functional `ox` (which i I am writting as ox in Haskell for “crossed O”):

ox :: [(x -> r) -> x] -> ([x] -> r) -> [x]
ox [] p = []
ox (e : es) p = a : ox es (p . (a:))
   where a = e (\x -> p (x : ox es (p . (x:))))

It is just four lines of code, so how complicated could it be? Well, read the paper to find out. If you are ready for serious math, have a look at this paper instead.

→ continue reading (3 comments)

After more than 1300 days of uninterrupted service, the good old PC that served the blog started to spontaneously reboot every 4 minutes or so. It looks like a hardware failure. I moved the site to a temporary machine. I am seriously considering renting a private virtual server and just forget about buying my own hardware in the future.

On top of that I discovered that evil forces planted a phishing attack on the blog about two weeks ago. The strategy was this:

1. Create an account on my blog (I stupidly left registration open to everyone).
2. Elevate account privileges to administrator by exploiting a WordPress security hole (I do not know which one).
3. Upload evil files to the upload area.
4. Direct phishing victims to the uploaded files.

So, keep your WordPress as closed as possible.

→ continue reading (3 comments)

I get asked every so often to release the source code for my random art project. The original source is written in Ocaml and is not publicly available, but here is a simple example of how you can get random art going in python in 250 lines of code.

Download source: randomart.py

→ continue reading (12 comments)

I am discovering that mathematicians cannot tell the difference between “proof by contradiction” and “proof of negation”. This is so for good reasons, but conflation of different kinds of proofs is bad mental hygiene which leads to bad teaching practice and confusion. For reference, here is a short explanation of the difference between proof of negation and proof by contradiction.

→ continue reading (24 comments)

It was time I changed the old blog style to something a bit more modern. I hope you like it.

Now I just have to figure out how to port 60 blog posts from ASCIIMathML notation to something a bit friendlier that can use MathML but does not require it. What is out there? I know about jsMath. I am open to suggestions.

→ continue reading (11 comments)

Already a while ago videolectures.net published this tutorial on Computer Verified Exact Analysis by Bas Spitters and Russell O'Connor from Computability and Complexity in Analysis 2009. I forgot to advertise it, so I am doing this now. It is about an implementation of exact real arithmetic whose correctness has been verified in Coq. Russell also gave a quick tutorial on Coq.

→ continue reading

With Davorin Lešnik.

Abstract: We investigate the relationship between the synthetic approach to topology, in which every set is equipped with an intrinsic topology, and constructive theory of metric spaces. We relate the synthetic notion of compactness of Cantor space to Brouwer's Fan Principle. We show that the intrinsic and metric topologies of complete separable metric spaces coincide if they do so for Baire space. In Russian Constructivism the match between synthetic and metric topology breaks down, as even a very simple complete totally bounded space fails to be compact, and its topology is strictly finer than the metric topology. In contrast, in Brouwer's intuitionism synthetic and metric notions of topology and compactness agree.

Download paper: csms_in_synthtop.pdf

→ continue reading

The following argument is often cited as an example of the necessity of the law of excluded middle and classical logic. We are supposed to demonstrate the existence of two irrational numbers $a$ and $b$ such that their power $a^b$ is rational. By the law of excluded middle, $\sqrt{2}^{\sqrt{2}}$ is rational or not. If it is rational, take $a = b = \sqrt{2}$, otherwise take $a = \sqrt{2}^{\sqrt{2}}$ and $b = \sqrt{2}$. In either case $a^b$ is rational. Let us think about this for a moment, from constructive point of view.

→ continue reading (18 comments)

In the last constructive gem we studied the exponential $2^\mathbb{N}$ and its isomorphic copies. This time we shall compute the double exponential $2^{2^\mathbb{N}}$ and even write some Haskell code.

→ continue reading (4 comments)

Constructive gems are usually not about particular results, because all constructive results can be proved classically as well, but rather about the method and the way of thinking. I demonstrate a constructive proof which can be reused in three different settings (set theory, topology, computability) because constructive mathematics has many different interpretations.

→ continue reading (28 comments)

I promise I will post a constructive gem soon. This constructive stone came up as a reaction to the cardinality of finite sets stone. I show that inhabited sets of natural numbers need not have minima, constructively.

→ continue reading

Cardinality of sets in constructive mathematics is not as well behaved as in classical mathematics. Cardinalities of finite sets are not natural numbers, and cardinalities are not linearly ordered.

→ continue reading (13 comments)

Just like in real life, constructive stones are easier to find than constructive gems, so let me start the series with a stone about constructive finite sets.

Two girl one cup
→ continue reading (3 comments)

In various mathematical forums, mostly those of a logical flavor, I regularly see people asking basic questions about constructive mathematics. I also see misconceptions about constructive mathematics. I shall make a series of posts, _Constructive Gems and Stone_s, which will answer basic questions about constructive mathematics, and will hopefully help fix wrong ideas about constructive mathematics.

A constructive gem is something nice about constructive mathematics that makes you want to know more about it. In contrast, a constructive stone is a complication in constructive mathematics which does not exist in the classical counterpart.

Here we go! The first one is about finite sets.

→ continue reading

These are the slides and the extended abstract from my MSFP 2008 talk. Apparently, I forgot to publish them online. There is a discussion on the Agda mailing list to which the talk is somewhat relevant, so I am publishing now.

Abstract: Realizability is an interpretation of intuitionistic logic which subsumes the Curry-Howard interpretation of propositions as types, because it allows the realizers to use computational effects such as non-termination, store and exceptions. Therefore, we can use realizability as a framework for program development and extraction which allows any style of programming, not just the purely functional one that is supported by the Curry-Howard correspondence. In joint work with Christopher A. Stone we developed RZ, a tool which uses realizability to translate specifications written in constructive logic into interface code annotated with logical assertions. RZ does not extract code from proofs, but allows any implementation method, from handwritten code to code extracted from proofs by other tools. In our experience, RZ is useful for specification of non-trivial theories. While the use of computational effects does improve efficiency it also makes it difficult to reason about programs and prove their correctness. We demonstrate this fact by considering non-purely functional realizers for a Brouwerian continuity principle.

Download: msfp2008-slides.pdf, msfp2008-abstract.pdf

→ continue reading (2 comments)

In a recent post I claimed that Python's lambda construct is broken. This attracted some angry responses by people who thought I was confused about how Python works. Luckily there were also many useful responses from which I learnt. This post is a response to comment 27, which asks me to say more about my calling certain design decisions in Python crazy.

→ continue reading (62 comments)

I quite like Python for teaching. And people praise it for the lambda construct which is a bit like $\lambda$-abstraction in functional languages. However, it is broken!

→ continue reading (57 comments)

I have been writing lecture notes on computable mathematics. One of the questions that came up was whether it is possible to simulate the booleans in the simply-typed $\lambda$-calculus. This is a nice puzzle in functional programming. If you solve it, definitely let me know, although I suspect logicians did it a long time ago.

→ continue reading (8 comments)

Abstract: In the effective topos there exists a chain-complete distributive lattice with a monotone and progressive endomap which does not have a fixed point. Consequently, the Bourbaki-Witt theorem and Tarski’s fixed-point theorem for chain-complete lattices do not have constructive (topos-valid) proofs.

Download: fixed-points.pdf

Published in: Theoretical Computer Science Volume 430, 27 April 2012, Pages 43–50. Mathematical Foundations of Programming Semantics (MFPS XXV)

→ continue reading (2 comments)

I have aded to the PL Zoo a mini prolog interpreter. It really is minimalistic, as it only handles pure Horn clauses. There is no arithmetic, lists, cuts, or disjunctions. Nevertheless, it ought to be possible to write a miniml interpreter in it... If anyone does it, please send me the code!

→ continue reading (1 comment)

This is a short note pointing out that the recent paper on“Mathematical undecidability and quantum randomness” by Tomasz Paterek et al. is no black magic, and that the authors are well aware of it. Unfortunately the paper appeared on Slashdot and has since generated an infinite amount of quasi-mathematical discussions.

→ continue reading (2 comments)

I have added two new languages to the PL Zoo. The minor addition is miniml+error, which is just MiniML with an error exception (raised by division by 0) that cannot be caught. The purpose is to demonstrate handling of fatal errors during runtime. The more interesting new animal is levy (written by Matija Pretnar and myself), an implementation of Paul Levy's call-by-push-value language. If you only know about Haskell's call-by-name and ML's call-by-value, I invite you to learn about call-by-push-value. Start by reading Paul's FAQ.

→ continue reading (1 comment)

I show how monads in Haskell can be used to structure infinite search algorithms, and indeed get them for free. This is a follow-up to my blog post Seemingly impossible functional programs. In the two papers Infinite sets that admit fast exhaustive search (LICS07) and Exhaustible sets in higher-type computation (LMCS08), I discussed what kinds of infinite sets admit exhaustive search in finite time, and how to systematically build such sets. Here I build them using monads, which makes the algorithms more transparent (and economic).

→ continue reading (14 comments)

Lately I've been thinking about computational effects in general, i.e., what is the structure of the “space of all computational effects”. We know very little about this topic. I am not even sure we know what “the space of all computational effects” is. Because Haskell is very popular and in Haskell computational effects are expressed as monads, many people might think that I am talking about the space of all monads. But I am not, and in this post I show two computational effects which are not of the usual Haskell monad kind. They should present a nice programming challenge to Haskell fans.

→ continue reading (14 comments)

Back in 2000 John Langford of the Machine Learning (Theory) blog and I wrote a backup script which I am still using today. A number of other people have found it useful so I decided to release it under an open source license. The script is easy to use under Linux. I am told it also backs up Windows with a bit of tweaking.

→ continue reading

I have added two new languages to the Programming Languages Zoo which demonstrate polymorphic type inference and type checking with subtypes.

→ continue reading (1 comment)

HERA is an implementation of exact real arithmetic in Haskell using the approach by Andrej Bauer and Iztok Kavkler, see these and these slides. It uses the fast multiple precision floating point library MPFR. Download source, and see documentation and examples of usage at my home page.

[Note by Andrej: this is a guest post by Aleš Bizjak, a first-year student of mathematics at my department. I am very proud of the excellent work he did on his summer project.]

→ continue reading

Two versions of this talk were given at Computability and complexity in analysis 2008 and at Mathematics, Algorithms and Proofs 2008.

Joint work with Paul Taylor.

Abstract: Cauchy's construction of reals as sequences of rational approximations is the theoretical basis for a number of implementations of exact real numbers, while Dedekind's construction of reals as cuts has inspired fewer useful computational ideas. Nevertheless, we can see the computational content of Dedekind reals by constructing them within Abstract Stone Duality (ASD), a computationally meaningful calculus for topology. This provides the theoretical background for a novel way of computing with real numbers in the style of logic programming. Real numbers are defined in terms of (lower and upper) Dedekind cuts, while programs are expressed as statements about real numbers in the language of ASD. By adapting Newton's method to interval arithmetic we can make the computations as efficient as those based on Cauchy reals.

Slides: slides-map2008.pdf (obsolete version: slides-cca2008.pdf)
Extended abstract: abstract-cca2098.pdf

→ continue reading

At MSFP 2008 in Iceland I chatted with Dan Piponi about physics and intuitionistic mathematics, and he encouraged me to write down some of the ideas. I have little, if anything, original to say, so this seems like an excellent opportunity for a blog post. So let me explain why I think intuitionistic mathematics is good for physics.

→ continue reading (37 comments)

I have added another language, called Boa, to the Programming Languages Zoo. It is an object-oriented language with the following features:

• integers and booleans as base types,
• first-class functions,
• dynamically typed,
• objects are extensible records with mutable fields,
• there are no classes, instead we can define “prototype” objects and extend them
  to create instances.

→ continue reading (2 comments)

I teach Theory of Programing Languages (page in Slovene). For the course I implemented languages which demonstrate basic concepts such as parsing, type checking, type inference, dynamic types, evaluation strategies, and compilation. My teaching assistant Iztok Kavkler contributed to the source code as well. I decided to publish the source code as a Programming Language Zoo for anyone who wants to know more about design and implementation of programming languages.

→ continue reading (1 comment)

Occasionally I hear claims that uncountable and uncomputable sets cannot be represented on computers. More generally, there are all sorts of misguided opinions about representations of data on computers, especially infinite data of mathematical nature. Here is a quick tutorial on the matter whose main point is:

It is meaningless to discuss representations of a set by a datatype without also considering operations that we want to perform on the set.

→ continue reading (11 comments)

Today I lectured about the Hydra game by Laurence Kirby and Jeff Paris (Accessible Independence Results for Peano Arithmetic, Kirby and Paris, Bull. London Math. Soc. 1982; 14: 285-293). For the occasion I implemented the game in Java. I am publishing the code for anyone who wants to play, or use it for teaching.

→ continue reading (23 comments)

Paul Taylor has published a revised version of his `lambda`-calculus for real analysis. I recommend it to anyone who is interested in real analysis, be it a computer scientist, numerical analyst, or just a “true” analyst.

The first, second, and third time I talked to Paul I could not understand a word of what he was saying, and that's not just because he is a native speaker of English English. I only began to “get it” when he visited me in Ljubljana. So I think it's perhaps worth explaining a bit what this “`lambda`-calculus for real analysis” is about.

→ continue reading (7 comments)

With Iztok Kavkler.

Abstract: We formulate a predicative, constructive theory of continuous domains whose realizability interpretation gives a practical implementation of continuous ω-chain complete posets and continuous maps between them. We apply the theory to implementation of the interval domain and exact real numbers.

Download: constructive-domains.pdf

→ continue reading

Andrej has invited me to write about certain surprising functional programs. The first program, due to Ulrich Berger (1990), performs exhaustive search over the “Cantor space” of infinite sequences of binary digits. I have included references at the end. A weak form of exhaustive search amounts to checking whether or not a total predicate holds for all elements of the Cantor space. Thus, this amounts to universal quantification over the Cantor space. Can this possibly be done algorithmically, in finite time?

→ continue reading (21 comments)

With Iztok Kavkler.

Abstract: The interval domain was proposed by Dana Scott as a domain-theoretic model for real numbers. It is a successful theoretical idea which also inspired a number of computational models for real numbers. However, current state-of-the-art implementations of real numbers, e.g., Mueller's iRRAM and Lambov's RealLib, do not seem to be based on the interval domain. In fact, their authors have observed that domain-theoretic concepts such as monotonicity of functions hinder efficiency of computation.

I will review the data structures and algorithms that are used in modern implementations of exact real arithmetic. They provide important insights, but some questions remain about what theoretical models support them, and how we can show them to be correct. It turns out that the correctness is not always clear, and that the good old interval domain still has a few tricks to offer.

Download slides: domains8-slides.pdf

→ continue reading (5 comments)

A tutorial presented at the Mathematical Foundations of Programming Semantics XXIII Tutorial Day.

→ continue reading (5 comments)

With Davorin Lešnik.

Abstract: We investigate the relationship between constructive theory of metric spaces and synthetic topology. Connections between these are established by requiring a relationship to exist between the intrinsic and the metric topology of a space. We propose a non-classical axiom which has several desirable consequences, e.g., that all maps between separable metric spaces are continuous in the sense of metrics, and that, up to topological equivalence, a set can be equipped with at most one metric which makes it complete and separable.

Presented at: 3rd Workshop on Formal Topology

Download slides: 3wft.pdf

→ continue reading

With Iztok Kavkler.

Abstract: RZ is a tool which translates axiomatizations of mathematical structures to program specifications using the realizability interpretation of logic. This helps programmers correctly implement data structures for computable mathematics. RZ does not prescribe a particular method of implementation, but allows programmers to write efficient code by hand, or to extract trusted code from formal proofs, if they so desire. We used this methodology to axiomatize real numbers and implemented the specification computed by RZ. The axiomatization is the standard domain-theoretic construction of reals as the maximal elements of the interval domain, while the implementation closely follows current state-of-the-art implementations of exact real arithmetic. Our results shows not only that the theory and practice of computable mathematics can coexist, but also that they work together harmoniously.

Presented at Computability and Complexity in Analysis 2007.

Download paper: rzreals.pdf

Download slides: cca2007-slides.pdf

→ continue reading

The famous theorem by Cantor states that the cardinality of a powerset $P(A)$ is larger than the cardinality of $A$. There are several equivalent formulations, and the one I want to consider is

Theorem (Cantor): There is no onto map $A \to P(A)$.

In this post I would like to analyze the usual proof of Cantor's theorem and present an insightful reformulation of it which has applications outside set theory.

→ continue reading (6 comments)

With Chris Stone.

Abstract:
Realizability theory is not only a fundamental tool in logic and computability, but also has direct application to the design and implementation of programs: it can produce interfaces for the data structure corresponding to a mathematical theory. Our tool, called RZ, serves as a bridge between the worlds of constructive mathematics and programming. By using the realizability interpretation of constructive mathematics, RZ translates specifications in constructive logic into annotated interface code in Objective Caml. The system supports a rich input language allowing descriptions of complex mathematical structures. RZ does not extract code from proofs, but allows any implementation method, from handwritten code to code extracted from proofs by other tools.

Presented at Computablity in Europe 2007.

Download paper:

• Long version: cie-long.pdf (January 29, 2007)
• Short version: cie-short.pdf (January 29, 2007)

Download slides: cie2007-slides.pdf

Download source code from RZ web page.

→ continue reading (3 comments)

Recently there has been a discussion (here, here, here, and here) on the Foundations of Mathematics mailing list about completeness of Peano arithmetic (PA) with respect to “small” sentences. Harvey Friedman made several conjectures of the following kind: “All true small sentences of PA are provable.” He proposed measures of smallness, such as counting the number of distinct variables or restricting the depth of terms. Here are some statistics concerning such statements.

→ continue reading (9 comments)

This year the International Mathematical Olympiad took place in Slovenia. I participated as one of the organizers (problem selection and coordination). It was probably one of the busiest and most exciting times of my life,

→ continue reading

With Alex Simpson.

Abstract: We present a constructive meta-theorem about sequential continuity which allows us to conclude from a constructive proof of existence of a function between complete metric spaces satisfying a given system of (functional) equations that there also exists a sequentially continuous function satisfying the system.

Presented at: Trends in Constructive mathematics, Frauenwörth am Chimsee, Germany, June 2006.

Download slides: continuity_begets_continuity_bavaria_slides.pdf

→ continue reading

For the benefit of the topology seminar audience at the math department of University of Ljubljana, I have written a self-contained explanation of the Kleene tree, which is an interesting object in computability theory. For the benefit of the rest of the planet, I am publishing it here.

→ continue reading (2 comments)

You may have heard at times that there are mathematicians who think that all functions are continuous. One way of explaining this is to show that all computable functions are continuous. The point not appreciated by many (even experts) is that the truth of this claim depends on what programming language we use.

→ continue reading (40 comments)

Spaces of higher-order functions are fascinating mathematical objects that we do not know enough about. What are they and what is known about them?

→ continue reading (3 comments)

With Chris Stone.

Presented at: Reliable Implementation of Real Number Algorithms: Theory and Practice, Dagstuhl Seminar 06021.

Abstract: see “Specifications via Realizability (CLASE)”.

Talk notes: rz-dagstuhl.pdf (handwritten notes of the talk with examples of how RZ works)

→ continue reading

Computer algebra systems (CAS), such as Mathematica, are complex systems that have been evolving for a couple of decades. They are advertised as advanced mathematical tools, and users expect them to be such. They are the next-generation calculators. But they also suffer from serious design flaws.

→ continue reading (6 comments)

At the EST training workshop in Fischbachau, Germany, I gave two lectures on syntehtic computability theory. This version of the talk contains material on recursive analysis which is not found in the MFPS XXI version of a similar talk.

Abstract:
Computability theory, which investigates computable functions and computable sets, lies at the foundation of logic and computer science. Its classical presentations usually involve a fair amount of Goedel encodings. Consequently, there have been a number of presentations of computability theory that aimed to present the subject in an abstract and conceptually pleasing way. We build on two such approaches, Hyland's effective topos and Richman's formulation in Bishop-style constructive mathematics, and develop basic computability theory, starting from a few simple axioms. Because we want a theory that resembles ordinary mathematics as much as possible, we never speak of Turing machines and Goedel encodings, but rather use familiar concepts from set theory and
topology.

Download slides: est.pdf

→ continue reading (8 comments)

A neat example of propositions-as-types using recursion. → continue reading (2 comments)

Lecture notes for my tutorial at Computability and Complexity in Analysis 2005, Kyoto. → continue reading (13 comments)

With Paul Taylor.

Abstract: Abstract Stone Duality (ASD) is an approach to topology that provides an abstract and conceptually satisfying account of topological spaces. The calculus of ASD reveals the computational content of various topological notions and suggests how to compute with them. The distinguishing feature of ASD is a direct axiomatisation in terms of spaces and maps, which does not rely on an underlying set-theoretic or topos-theoretic foundation.

This paper makes the first step in real analysis within ASD, namely the construction of the real line using two-sided Dedekind cuts. Compactness and overtness of the closed interval are proved, and the arithmetic operations are defined. The ASD calculus gives programs for computing the arithmetic operations and the quantifiers that express compactness and overtness.

As the paper aims to be a self-contained introduction to ASD for those interested in constructive and computable topology and analysis, it includes a rapid survey of the ASD calculus. The foundational background to the calculus was covered in detail in earlier work.

Further topics in real analysis within ASD, such as the Intermediate Value Theorem, are presented in a separate paper by Paul Taylor which builds on this one.

To be presented at Computability and Complexity in Analysis 2005, Kyoto, Japan.

Download: an up-to-date version from Paul Taylor's Abstract Stone Duality page.

→ continue reading (3 comments)

So I decided to put all my research papers on the blog. → continue reading

The new address for Math and Computation blog is math.andrej.com → continue reading

In constructive mathematics even very small sets can be quite a bit more interesting than in classical mathematics. Since you will not believe me that sets with at most one element are very interesting, let us look at the set of truth values, which has “two” elements.

→ continue reading (18 comments)

What constructive mathematics actually says about the law of excluded middle. → continue reading (8 comments)

I have found a good way to write math in web pages. ASCIIMathML is a piece of javascript that translates simple-minded Latex-like ASCII math to MathML, but only if the browser supports MathML. Since the input syntax is very simple, the expressions are quite readable in the raw form, as well.

For example, if I type

`forall x in RR exists y in CC. (1-x^2 )/sqrt(1+y^4)=1`

it is seen as `forall x in RR exists y in CC. (1-x^2 )/sqrt(1+y^4)=1`. If you are going to post to the blog, you may be interested in the ASCIIMathML syntax reference page.

To enable MathML on your computer, install mathplayer plugin
if you are using Internet Explorer. For Firefox and Mozilla, you have to install math fonts.

→ continue reading (2 comments)

Abstract: Computability theory, which investigates computable functions and computable sets, lies at the foundation of computer science. Its classical presentations usually involve a fair amount of Gödel encodings which sometime obscure ingenious arguments. Consequently, there have been a number of presentations of computability theory that aimed to present the subject in an abstract and conceptually pleasing way. We build on two such approaches, Hyland's effective topos and Richman's formulation in Bishop-style constructive mathematics, and develop basic computability theory, starting from a few simple axioms. Because we want a theory that resembles ordinary mathematics as much as possible, we never speak of Turing machines and Gödel encodings, but rather use familiar concepts from set theory and topology.

Presented at: Mathematical Foundations of Programming Semantics XXI, Birmingham, 2004 (invited talk).

Download paper: synthetic.pdf, synthetic.ps.gz

Download slides: synthetic-slides.pdf

→ continue reading (1 comment)

I recently stumbled upon a blog on machine learning by a good friend of mine, John Langford. The blog has gathered together a community of people who discuss various topics (not limited strictly to machine learning). Naturally I wanted to have a blog, too.

I devote a lot of my time to thinking about the relationship between mathematics and computation. There are two sides of this, which can be expressed by a the slogan “Computable mathematics and mathematics of computation”. Computable mathematics is about how to do mathematics with computers, while mathematics of computation is about mathematics that describes properties of computation in a mathematical, abstract way.

If this is a subject that interests you, I invite you to join me.

→ continue reading (2 comments)

How to build specifications for abstract data types using realizability → continue reading

With Alex Simpson.

Abstract: We prove two embedding and extension theorems in the context of the constructive theory of metric spaces. The first states that Cantor space embeds in any inhabited complete separable metric space (CSM) without isolated points, `X`, in such a way that every sequentially continuous function from Cantor space to `ZZ` extends to a sequentially continuous function from `X` to `RR`. The second asserts an analogous property for Baire space relative to any inhabited locally non-compact CSM. Both results rely on having careful constructive formulations of the concepts involved.

As a first application, we derive new relationships between “continuity principles” asserting that all functions between specified metric spaces are pointwise continuous. In particular, we give conditions that imply the failure of the continuity principle “all functions from `X` to `RR` are continuous”, when `X` is an inhabited CSM without isolated points, and when `X` is an inhabited locally non-compact CSM. One situation in which the latter case applies is in models based on “domain realizability”, in which the failure of the continuity principle for any inhabited locally non-compact CSM, `X`, generalizes a result previously obtained by Escardo and Streicher in the special case `X = C[0,1]`.

As a second application, we show that, when the notion of inhabited complete separable metric space without isolated points is interpreted in a recursion-theoretic setting, then, for any such space `X`, there exists a Banach-Mazur computable function from `X` to the computable real numbers that is not Markov computable. This generalizes a result obtained by Hertling in the special case that `X` is the space of computable real numbers.

Published in: Mathematical Logic Quarterly, 50(4,5):351-369, 2004.

Download: continuity.pdf, continuity.ps.gz

→ continue reading

With Steve Awodey.

Abstract: Image factorizations in regular categories are stable under pullbacks, so they model a natural modal operator in dependent type theory. This unary type constructor `[A]` has turned up previously in a syntactic form as a way of erasing computational content, and formalizing a notion of proof irrelevance. Indeed, semantically, the notion of a support is sometimes used as surrogate proposition asserting inhabitation of an indexed family.

We give rules for bracket types in dependent type theory and provide complete semantics using regular categories. We show that dependent type theory with the unit type, strong extensional equality types, strong dependent sums, and bracket types is the internal type theory of regular categories, in the same way that the usual dependent type theory with dependent sums and products is the internal type theory of locally cartesian closed categories.

We also show how to interpret first-order logic in type theory with brackets, and we make use of the translation to compare type theory with logic. Specifically, we show that the propositions-as-types interpretation is complete with respect to a certain fragment of intuitionistic first-order logic. As a consequence, a modified double-negation translation into type theory (without bracket types) is complete for all of classical first-order logic.

Published in: Journal of Logic and Computation. Volume 14, Issue 4, August 2004, pp. 447-471.

Download: bracket_types.pdf, bracket_types.ps.gz

→ continue reading (2 comments)

Abstract: In this paper I compare two well studied approaches to topological semantics—the domain-theoretic approach, exemplified by the category of countably based equilogical spaces, `omega`Equ, and Type Two Effectivity, exemplified by the category of Baire space representations, Rep(B). These two categories are both locally cartesian closed extensions of countably based `T_0`-spaces. A natural question to ask is how they are related.

First, we show that Rep(B) is equivalent to a full coreflective subcategory of `omega`Equ, consisting of the so-called `0`-equilogical spaces. This establishes a pair of adjoint functors between Rep(B) and `omega`Equ. The inclusion of Rep(B) in `omega`Equ and its coreflection have many desirable properties, but they do not preserve exponentials in general. This means that the cartesian closed structures of Rep(B) and `omega`Equ are essentially different. However, in a second comparison we show that Rep(B) and `omega`Equ do share a common cartesian closed subcategory that contains all countably based `T_0`-spaces. Therefore, the domain-theoretic approach and TTE yield equivalent topological semantics of computation for all higher-order types over countably based `T_0`-spaces. We consider several examples involving the natural numbers and the real numbers to demonstrate how these comparisons make it possible to transfer results from one setting to another.

Published in: Mathematical logic quarterly, 2002, vol. 48, suppl. 1, 1-15.

Download: equtte.pdf, equtte.ps.gz

→ continue reading

With Lars Birkedal and Dana Scott.

Abstract: It is well known that one can build models of full higher-order dependent type theory (also called the calculus of constructions) using partial equivalence relations (PERs) and assemblies over a partial combinatory algebra (PCA). But the idea of categories of PERs and ERs (total equivalence relations) can be applied to other structures as well. In particular, we can easily define the category of ERs and equivalence-preserving continuous mappings over the standard category Top of topological `T_0`-spaces; we call these spaces (a topological space together with an ER) equilogical spaces and the resulting category Equ. We show that this category—in contradistinction to Top—is a cartesian closed category. The direct proof outlined here uses the equivalence of the category Equ to the category PEqu of PERs over algebraic lattices (a full subcategory of Top that is well known to be cartesian closed from domain theory). In another paper with Carboni and Rosolini (cited herein) a more abstract categorical generalization shows why many such categories are cartesian closed. The category Equ obviously contains Top as a full subcategory, and it naturally contains many other well known subcategories. In particular, we show why, as a consequence of work of Ershov, Berger, and others, the Kleene-Kreisel hierarchy of countable functionals of finite types can be naturally constructed in Equ from the natural numbers object `N` by repeated use in Equ of exponentiation and binary products. We also develop for Equ notions of modest sets (a category equivalent to Equ) and assemblies to explain why a model of dependent type theory is obtained. We make some comparisons of this model to other, known models.

Published in: Theoretical Computer Science, 315(1):35-59, 2004.

Download: equ.pdf, equ.ps.gz.

→ continue reading

With Alex Simpson and Martín Escardó.

Abstract: We compare the definability of total functionals over the reals in two functional-programming approaches to exact real-number computation: the extensional approach, in which one has an abstract datatype of real numbers; and the intensional approach, in which one encodes real numbers using ordinary datatypes. We show that the type hierarchies coincide for second-order types, and we relate this fact to an analogous comparison of type hierarchies over the external and internal real numbers in Dana Scott's category of equilogical spaces. We do not know whether similar coincidences hold at third-order types. However, we relate this question to a purely topological conjecture about the Kleene-Kreisel continuous functionals over the natural numbers. Finally, we demonstrate that, in the intensional approach to exact real-number computation, parallel primitives are not required for programming second-order total functionals over the reals.

Published in: In Proceedings ICALP 2002, Springer LNCS 2380, pp. 488-500, 2002.

Download: paradigms.pdf, paradigms.ps.gz, paradigms_proofs.ps.gz (long version, with proofs)

→ continue reading

with Steve Awodey.

Abstract: We compare realizability models over partial combinatory algebras by embedding them into sheaf toposes. We then use the machinery of Grothendieck toposes and geometric morphisms to study the relationship between realizability models over different partial combinatory algebras. This research is part of the Logic of Types and Computation project at Carnegie Mellon University under the direction of Dana Scott.

Sumitted for publication.

Download: sheaves_realizability.pdf, sheaves_realizability.ps.gz

→ continue reading

This is my Ph.D. dissertation, which I forgot to post on this blog. So I am doing it now. → continue reading

with Lars Birkedal.

Abstract: We show that dependent sums and dependent products of continuous parametrizations on domains with dense, codense, and natural totalities agree with dependent sums and dependent products in equilogical spaces, and thus also in the realizability topos `RT(P(NN))`.

Published in: In Proceedings of Computer Science Logic 2000, Lecture Notes in Computer Science, Vol. 1862, Editors: P.G. Clote, H. Schwichtenberg, Springer, August 2000, pp. 202-216.

Download: dependent_functionals.pdf, dependent_functionals.ps.gz

→ continue reading

with Marko Petkovšek.

Abstract: Gosper's summation algorithm finds a hypergeometric closed form of an indefinite sum of hypergeometric terms, if such a closed form exists. We extend the algorithm to the case when the terms are simultaneously hypergeometric and multibasic hypergeometric. We also provide algorithms for finding polynomial as well as hypergeometric solutions to recurrences in the mixed case. We do not require the based to be transcedental, but only that `q_1^(k_1) . . . q_m^(k_m) != 1` unless `k_1 = ... = k_m = 0`. Finally, we generalize the concept of greatest factorial factorization to the mixed hypergeometric case.

Published in: Journal of Symbolic Computation, Vol. 28 (1999) 711-736.

Download: gengosper.pdf, gengosper.ps.gz

→ continue reading

with Edmund Clarke and Xudong Zhao.

Abstract: Analytica is an automatic theorem prover for theorems in elementary analysis. The prover is written in Mathematica language and runs in the Mathematica environment. The goal of the project is to use a powerful symbolic computation system to prove theorems that are beyond the scope of previous automatic theorem provers. The theorem prover is also able to deduce correctness of certain simplification steps that would otherwise not be performed. We describe the structure of Analytica and explain the main techniques that it uses to construct proofs. Analytica has been able to prove several non-trivial theorems. In this paper, we show how it can prove a series of lemmas that lead to Bernstein approximation theorem.

Published in: Journal of Automated Reasoning, Vol. 21, no.3 (1998) 295-325

Download: analytica.pdf, analytica.ps.gz

Source code: analytica.tar.gz contains the source code for Analytica. It works under Mathematica 2.2.2. I do not plan to port it to a newer version of Mathematics. If you do that, please let me know.

→ continue reading