In 1890 Giuseppe Peano discovered a square-filling curve, and a year later David Hilbert published his variation. In those days people did not waste readers' attention with dribble – Peano explained it all on 3 pages, and Hilbert on just 2 pages, with a picture!

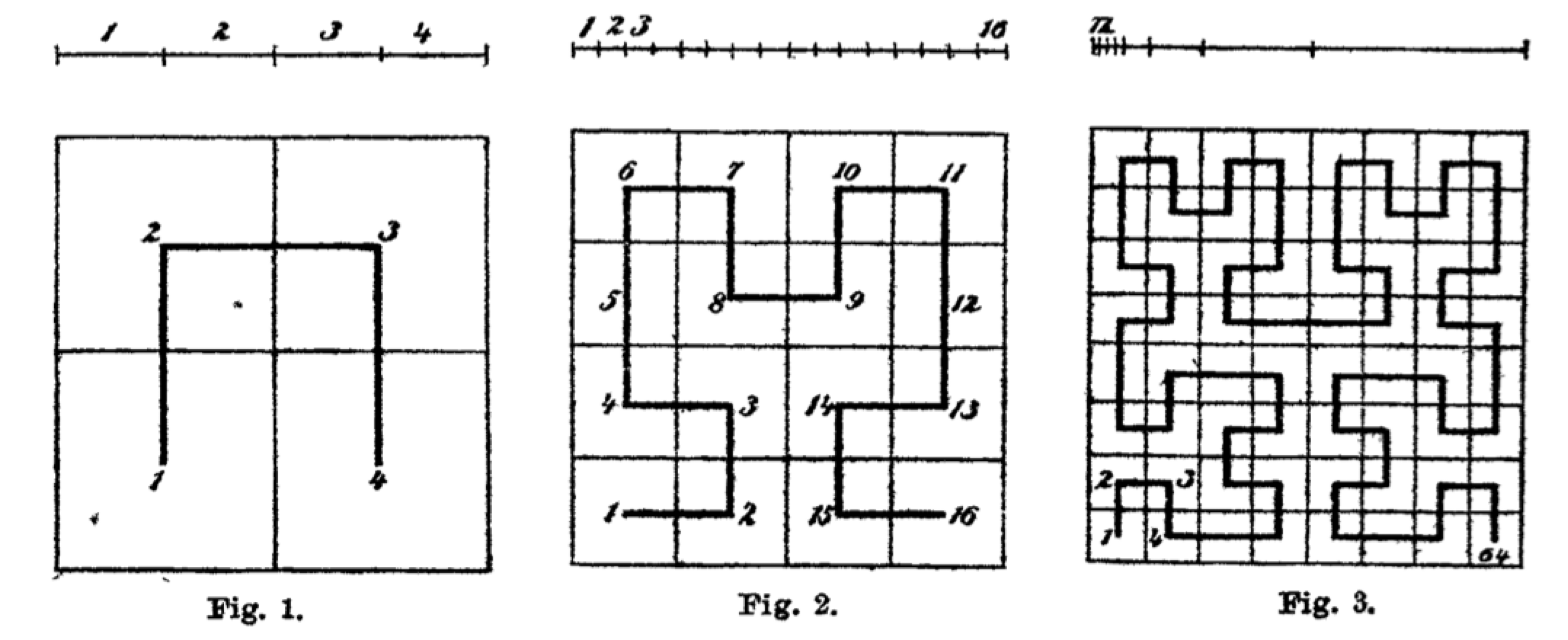
But are these constructive square-filling curves?

→ continue reading

On the occasion of Dieter Spreen's 75th birthday there will be a Festschrift in the Journal of Logic and Analysis. I have submitted a paper “Spreen spaces and the synthetic Kreisel-Lacombe-Shoenfield-Tseitin theorem”, available as a preprint arXiv:2307.07830, that develops a constructive account of Dieter's generalization of a famous theorem about continuity of computable functions. In this post I explain how the paper fits into the more general topic of continuity principles.

→ continue reading

On February 10, 2023, I gave my Levi L. Conant Lectur Series talk “Exploring strange new worlds of mathematics”, at the math department of Worcester Polytechnic Institute. Here are the slides with speaker notes and the video recording of the talk.

→ continue reading

Jacques Carette asked on Twitter for a refence to the fact that countable choice holds in setoids. I then spent a day formalizing facts about the axiom of choice in setoids in Agda. I noticed something interesting that is worth blogging about.

→ continue reading (4 comments)

A while ago, my former student Chuangjie Xu and I computed an integer using a sheaf topos. For that purpose,

1. we developed our mathematics constructively,
2. we formalized our mathematics in Martin-Löf type theory, in Agda notation,
3. we pressed a button, and
4. after a few seconds we saw the integer we expected in front of us.

Well, it was a few seconds for the computer in steps (3)-(4), but three years for us in steps (1)-(2).

→ continue reading

This is joint work with Marc Bezem, Thierry Coquand, Peter Dybjer.

We use the Burali-Forti argument to show that, in homotopy type theory and univalent foundations, the embedding $$ \mathcal{U} \to \mathcal{U}^+$$ of a universe $\mathcal{U}$ into its successor $\mathcal{U}^+$ is not an equivalence. We also establish this for the types of sets, magmas, monoids and groups. The arguments in this post are also written in Agda.

→ continue reading

Joel Hamkins advertised the following theorem on Twitter:

Theorem: All complete ordered fields are isomorphic.

The standard proof posted by Joel has two parts:

1. A complete ordered field is archimedean.
2. Using the fact that the rationals are dense in an archimedean field, we construct an isomorphism between any two complete ordered fields.

The second step is constructive, but the first one is proved using excluded middle, as follows. Suppose $F$ is a complete ordered field. If $b \in F$ is an upper bound for the natural numbers, construed as a subset of $F$, then so $b - 1$, but then no element of $F$ can be the least upper bound of $\mathbb{N}$. By excluded middle, above every $x \in F$ there is $n \in \mathbb{N}$.

So I asked myself and the constructive news mailing list what the constructive status of the theorem is. But something was amiss, as Fred Richman immediately asked me to provide an example of a complete ordered field. Why would he do that, don't we have the MacNeille reals? After agreeing on definitions, Toby Bartels gave the answer, which I am taking the liberty to adapt a bit and present here. I am probably just reinventing the wheel, so if someone knows an original reference, please provide it in the comments.

The theorem holds constructively, but for a bizarre reason: if there exists a complete ordered field, then the law of excluded middle holds, and the standard proof is valid!

→ continue reading (11 comments)

In 2013 I gave a talk about constructive mathematics “Five stages of accepting constructive mathematics” (video) at the Institute for Advanced Study. I turned the talk into a paper, polished it up a bit, added things here and there, and finally it has now been published in the Bulletin of the American Mathematical Society. It is not quite a survey paper, but it is not very technical either. I hope you will enjoy reading it.

Free access to the paper:  Five stages of accepting constructive mathematics (PDF)

→ continue reading (12 comments)

I have not written a blog post in a while, so I decided to write up a short observation about truth values in intuitionistic logic which sometimes seems a bit puzzling.

Let $\Omega$ be the set of truth values (in Coq this would be the setoid whose underlying type is $\mathsf{Prop}$ and equality is equivalence $\leftrightarrow$, while in HoTT it is the h-propostions). Call a truth value $p : \Omega$ intermediate if it is neither true nor false, i.e., $p \neq \bot$ and $p \neq \top$. Such a “third” truth value $p$ is proscribed by excluded middle.

The puzzle is to explain how the following two facts fit together:

1. “There is no intermediate truth value” is an intuitionistic theorem.
2. There are models of intuitionistic logic with many truth values.

→ continue reading (6 comments)

Here are the slides from my Logic Coloquium 2014 talk in Vienna. This is joint work with Kazuto Yoshimura from Japan Advanced Institute for Science and Technology.

Abstract: In constructive mathematics we often consider implications between non-constructive reasoning principles. For instance, it is well known that the Limited principle of omniscience implies that equality of real numbers is decidable. Most such reductions proceed by reducing an instance of the consequent to an instance of the antecedent. We may therefore define a notion of instance reducibility, which turns out to have a very rich structure. Even better, under Kleene's function realizability interpretation instance reducibility corresponds to Weihrauch reducibility, while Kleene's number realizability relates it to truth-table reducibility. We may also ask about a constructive treatment of other reducibilities in computability theory. I shall discuss how one can tackle Turing reducibility constructively via Kleene's number realizability.

Slides with talk notes:  lc2014-slides-notes.pdf

→ continue reading

In the post Seemingly impossible functional programs, I wrote increasingly efficient Haskell programs to realize the mathematical statement

$\forall p : X \to 2. (\exists x:X.p(x)=0) \vee (\forall x:X.p(x)=1)$

for $X=2^\mathbb{N}$, the Cantor set of infinite binary sequences, where $2$ is the set of binary digits. Then in the post A Haskell monad for infinite search in finite time I looked at ways of systematically constructing such sets $X$ with corresponding Haskell realizers of the above omniscience principle.

In this post I give examples of infinite sets $X$ and corresponding constructive proofs of their omniscience that are intended to be valid in Bishop mathematics, and which I have formalized in Martin-Löf type theory in Agda notation. This rules out the example $X=2^\mathbb{N}$, as discussed below, but includes many interesting infinite examples. I also look at ways of constructing new omniscient sets from given ones. Such sets include, in particular, ordinals, for which we can find minimal witnesses if any witness exists.

Agda is a dependently typed functional programming language based on Martin-Löf type theory. By the Curry-Howard correspondence, Agda is also a language for formulating mathematical theorems (types) and writing down their proofs (programs). Agda acts as a thorough referee, only accepting correct theorems and proofs. Moreover, Agda can run your proofs. Here is a graph of the main Agda modules for this post, and here is a full graph with all modules.

→ continue reading (1 comment)

In the HoTT book issue 460 a question by gluttonousGrandma (where do people get these nicknames?) once more exposed a common misunderstanding that we tried to explain in section 5.8 of the book (many thanks to Bas Spitters for putting the book into Google Books so now we can link to particular pages). Apparently the following belief is widely spread, and I admit to holding it a couple of years ago:

An inductive type contains exactly those elements that we obtain by repeatedly using the constructors.

If you believe the above statement you should keep reading. I am going to convince you that the statement is unfounded, or that at the very least it is preventing you from understanding type theory.

→ continue reading (29 comments)

The HoTT book is finished!

Since spring, and even before that, I have participated in a great collaborative effort on writing a book on Homotopy Type Theory. It is finally finished and ready for public consumption. You can get the book freely at http://homotopytypetheory.org/book/. Mike Shulman has written about the contents of the book, so I am not going to repeat that here. Instead, I would like to comment on the socio-technological aspects of making the book, and in particular about what we learned from open-source community about collaborative research.

→ continue reading (10 comments)

It seems to me that people think I am a constructive mathematician, or worse a constructivist (a word which carries a certain amount of philosophical stigma). Let me be perfectly clear: it is not decidable whether I am a constructive mathematician.

→ continue reading (44 comments)

It is well known that, both in constructive mathematics and in programming languages, types are secretly topological spaces and functions are secretly continuous. I have previously exploited this in the posts Seemingly impossible functional programs and A Haskell monad for infinite search in finite time, using the language Haskell. In languages based on Martin-Löf type theory such as Agda, there is a set of all types. This can be used to define functions $\mathbb{N} \to \mathrm{Set}$ that map numbers to types, functions $\mathrm{Set} \to \mathrm{Set}$ that map types to types, and so on.

Because $\mathrm{Set}$ itself is a type, a large type of small types, it must have a secret topology. What is it? There are a number of ways of approaching topology. The most popular one is via open sets. For some spaces, one can instead use convergent sequences, and this approach is more convenient in our situation. It turns out that the topology of the universe $\mathrm{Set}$ is indiscrete: every sequence of types converges to any type! I apply this to deduce that $\mathrm{Set}$ satisfies the conclusion of Rice's Theorem: it has no non-trivial, extensional, decidable property.

To see how this works, check:

• A short paper with the proofs in mathematical vernacular, and further discussion of the intuitions, motivations and consequences.
• Literate proofs in Agda of the universe indiscreteness theorem and Rice's Theorem for the universe.
• Agda proofs of related facts.

The Agda pages can be navigated be clicking at any (defined) symbol or word, in particular by clicking at the imported module names.

→ continue reading (2 comments)

With Peter LeFanu Lumsdaine.

Abstract: The Bourbaki-Witt principle states that any progressive map on a chain-complete poset has a fixed point above every point. It is provable classically, but not intuitionistically. We study this and related principles in an intuitionistic setting. Among other things, we show that Bourbaki-Witt fails exactly when the trichotomous ordinals form a set, but does not imply that fixed points can always be found by transfinite iteration. Meanwhile, on the side of models, we see that the principle fails in realisability toposes, and does not hold in the free topos, but does hold in all cocomplete toposes.

Download paper: bw.pdf
ArXiv version: arXiv:1201.0340v1 [math.CT]

This paper is an extension of my previous paper on the Bourbaki-Witt and Knaster-Tarski fixed-point theorems in the effective topos (arXiv:0911.0068v1).

→ continue reading

I am not sure whether to call this one a constructive gem or stone. I suppose it is a matter of personal taste. I think it is a gem, albeit a very unusual one: there is a topos in which $\mathbb{N}^\mathbb{N}$ can be embedded into $\mathbb{N}$.

→ continue reading (3 comments)

As a preparation for my part of a joint tutorial Programs from proofs at MFPS 27 at the end of this month with Ulrich Berger, Monika Seisenberger, and Paulo Oliva, I've developed in Agda some things we've been doing together.

Using

• Berardi-Bezem-Coquand functional, or alternatively,
• Berger-Oliva modified bar recursion, or alternatively,
• Escardo-Oliva countable product of selection functions,

for giving a proof term for classical countable choice, we prove the classical infinite pigeonhole principle in Agda: every infinite boolean sequence has a constant infinite subsequence, where the existential quantification is classical (double negated).

As a corollary, we get the finite pigeonhole principle, using Friedman's trick to make the existential quantifiers intuitionistic.

This we can run, and it runs fast enough. The point is to illustrate in Agda how we can get witnesses from classical proofs that use countable choice. The finite pigeonhole principle has a simple constructive proof, of course, and hence this is really for illustration only.

The main Agda files are

• InfinitePigeon
• FinitePigeon
• Examples

These are Agda files converted to html so that you can navigate them by clicking at words to go to their definitions. A zip file with all Agda files is available. Not much more information is available here.

The three little modules that implement the Berardi-Bezem-Coquand, Berger-Oliva and Escardo-Oliva functionals disable the termination checker, but no other module does. The type of these functionals in Agda is the J-shift principle, which generalizes the double-negation shift.

→ continue reading (3 comments)

Jens Blanck and I presented a paper at Computability and Complexity in Analysis 2009 with a complicated title (I like complicated titles):

Canonical Effective Subalgebras of Classical Algebras as Constructive Metric Completions

which has been published in Volume 16, Issue 18 of the Journal of Universal Computer Science. I usually just post the abstract, but this time I would like to explain the general idea informally, the way one can do it on a blog. But first, here is the abstract:

Abstract: We prove general theorems about unique existence of effective subalgebras of classical algebras. The theorems are consequences of standard facts about completions of metric spaces within the framework of constructive mathematics, suitably interpreted in realizability models. We work with general realizability models rather than with a particular model of computation. Consequently, all the results are applicable in various established schools of computability, such as type 1 and type 2 effectivity, domain representations, equilogical spaces, and others.

Download paper: effalg.pdf or directly from JUCS

→ continue reading (1 comment)

I think I am getting addicted to Coq, or more generally to doing mathematics, including the proofs, with computers. I spent last week finalizing a formalization of Gödel's functional interpretation of logic, also known as the Dialectica interpretation. There does not seem to be one available already, which is a good opportunity for a blog post.

→ continue reading (6 comments)

Already a while ago videolectures.net published this tutorial on Computer Verified Exact Analysis by Bas Spitters and Russell O'Connor from Computability and Complexity in Analysis 2009. I forgot to advertise it, so I am doing this now. It is about an implementation of exact real arithmetic whose correctness has been verified in Coq. Russell also gave a quick tutorial on Coq.

→ continue reading

With Davorin Lešnik.

Abstract: We investigate the relationship between the synthetic approach to topology, in which every set is equipped with an intrinsic topology, and constructive theory of metric spaces. We relate the synthetic notion of compactness of Cantor space to Brouwer's Fan Principle. We show that the intrinsic and metric topologies of complete separable metric spaces coincide if they do so for Baire space. In Russian Constructivism the match between synthetic and metric topology breaks down, as even a very simple complete totally bounded space fails to be compact, and its topology is strictly finer than the metric topology. In contrast, in Brouwer's intuitionism synthetic and metric notions of topology and compactness agree.

Download paper: csms_in_synthtop.pdf

→ continue reading

The following argument is often cited as an example of the necessity of the law of excluded middle and classical logic. We are supposed to demonstrate the existence of two irrational numbers $a$ and $b$ such that their power $a^b$ is rational. By the law of excluded middle, $\sqrt{2}^{\sqrt{2}}$ is rational or not. If it is rational, take $a = b = \sqrt{2}$, otherwise take $a = \sqrt{2}^{\sqrt{2}}$ and $b = \sqrt{2}$. In either case $a^b$ is rational. Let us think about this for a moment, from constructive point of view.

→ continue reading (18 comments)

These are the slides and the extended abstract from my MSFP 2008 talk. Apparently, I forgot to publish them online. There is a discussion on the Agda mailing list to which the talk is somewhat relevant, so I am publishing now.

Abstract: Realizability is an interpretation of intuitionistic logic which subsumes the Curry-Howard interpretation of propositions as types, because it allows the realizers to use computational effects such as non-termination, store and exceptions. Therefore, we can use realizability as a framework for program development and extraction which allows any style of programming, not just the purely functional one that is supported by the Curry-Howard correspondence. In joint work with Christopher A. Stone we developed RZ, a tool which uses realizability to translate specifications written in constructive logic into interface code annotated with logical assertions. RZ does not extract code from proofs, but allows any implementation method, from handwritten code to code extracted from proofs by other tools. In our experience, RZ is useful for specification of non-trivial theories. While the use of computational effects does improve efficiency it also makes it difficult to reason about programs and prove their correctness. We demonstrate this fact by considering non-purely functional realizers for a Brouwerian continuity principle.

Download: msfp2008-slides.pdf, msfp2008-abstract.pdf

→ continue reading (2 comments)

Abstract: In the effective topos there exists a chain-complete distributive lattice with a monotone and progressive endomap which does not have a fixed point. Consequently, the Bourbaki-Witt theorem and Tarski’s fixed-point theorem for chain-complete lattices do not have constructive (topos-valid) proofs.

Download: fixed-points.pdf

Published in: Theoretical Computer Science Volume 430, 27 April 2012, Pages 43–50. Mathematical Foundations of Programming Semantics (MFPS XXV)

→ continue reading (2 comments)

I show how monads in Haskell can be used to structure infinite search algorithms, and indeed get them for free. This is a follow-up to my blog post Seemingly impossible functional programs. In the two papers Infinite sets that admit fast exhaustive search (LICS07) and Exhaustible sets in higher-type computation (LMCS08), I discussed what kinds of infinite sets admit exhaustive search in finite time, and how to systematically build such sets. Here I build them using monads, which makes the algorithms more transparent (and economic).

→ continue reading (14 comments)

Two versions of this talk were given at Computability and complexity in analysis 2008 and at Mathematics, Algorithms and Proofs 2008.

Joint work with Paul Taylor.

Abstract: Cauchy's construction of reals as sequences of rational approximations is the theoretical basis for a number of implementations of exact real numbers, while Dedekind's construction of reals as cuts has inspired fewer useful computational ideas. Nevertheless, we can see the computational content of Dedekind reals by constructing them within Abstract Stone Duality (ASD), a computationally meaningful calculus for topology. This provides the theoretical background for a novel way of computing with real numbers in the style of logic programming. Real numbers are defined in terms of (lower and upper) Dedekind cuts, while programs are expressed as statements about real numbers in the language of ASD. By adapting Newton's method to interval arithmetic we can make the computations as efficient as those based on Cauchy reals.

Slides: slides-map2008.pdf (obsolete version: slides-cca2008.pdf)
Extended abstract: abstract-cca2098.pdf

→ continue reading

At MSFP 2008 in Iceland I chatted with Dan Piponi about physics and intuitionistic mathematics, and he encouraged me to write down some of the ideas. I have little, if anything, original to say, so this seems like an excellent opportunity for a blog post. So let me explain why I think intuitionistic mathematics is good for physics.

→ continue reading (37 comments)

With Iztok Kavkler.

Abstract: We formulate a predicative, constructive theory of continuous domains whose realizability interpretation gives a practical implementation of continuous ω-chain complete posets and continuous maps between them. We apply the theory to implementation of the interval domain and exact real numbers.

Download: constructive-domains.pdf

→ continue reading

With Iztok Kavkler.

Abstract: The interval domain was proposed by Dana Scott as a domain-theoretic model for real numbers. It is a successful theoretical idea which also inspired a number of computational models for real numbers. However, current state-of-the-art implementations of real numbers, e.g., Mueller's iRRAM and Lambov's RealLib, do not seem to be based on the interval domain. In fact, their authors have observed that domain-theoretic concepts such as monotonicity of functions hinder efficiency of computation.

I will review the data structures and algorithms that are used in modern implementations of exact real arithmetic. They provide important insights, but some questions remain about what theoretical models support them, and how we can show them to be correct. It turns out that the correctness is not always clear, and that the good old interval domain still has a few tricks to offer.

Download slides: domains8-slides.pdf

→ continue reading (5 comments)

A tutorial presented at the Mathematical Foundations of Programming Semantics XXIII Tutorial Day.

→ continue reading (5 comments)

With Davorin Lešnik.

Abstract: We investigate the relationship between constructive theory of metric spaces and synthetic topology. Connections between these are established by requiring a relationship to exist between the intrinsic and the metric topology of a space. We propose a non-classical axiom which has several desirable consequences, e.g., that all maps between separable metric spaces are continuous in the sense of metrics, and that, up to topological equivalence, a set can be equipped with at most one metric which makes it complete and separable.

Presented at: 3rd Workshop on Formal Topology

Download slides: 3wft.pdf

→ continue reading

With Iztok Kavkler.

Abstract: RZ is a tool which translates axiomatizations of mathematical structures to program specifications using the realizability interpretation of logic. This helps programmers correctly implement data structures for computable mathematics. RZ does not prescribe a particular method of implementation, but allows programmers to write efficient code by hand, or to extract trusted code from formal proofs, if they so desire. We used this methodology to axiomatize real numbers and implemented the specification computed by RZ. The axiomatization is the standard domain-theoretic construction of reals as the maximal elements of the interval domain, while the implementation closely follows current state-of-the-art implementations of exact real arithmetic. Our results shows not only that the theory and practice of computable mathematics can coexist, but also that they work together harmoniously.

Presented at Computability and Complexity in Analysis 2007.

Download paper: rzreals.pdf

Download slides: cca2007-slides.pdf

→ continue reading

With Alex Simpson.

Abstract: We present a constructive meta-theorem about sequential continuity which allows us to conclude from a constructive proof of existence of a function between complete metric spaces satisfying a given system of (functional) equations that there also exists a sequentially continuous function satisfying the system.

Presented at: Trends in Constructive mathematics, Frauenwörth am Chimsee, Germany, June 2006.

Download slides: continuity_begets_continuity_bavaria_slides.pdf

→ continue reading

For the benefit of the topology seminar audience at the math department of University of Ljubljana, I have written a self-contained explanation of the Kleene tree, which is an interesting object in computability theory. For the benefit of the rest of the planet, I am publishing it here.

→ continue reading (2 comments)

You may have heard at times that there are mathematicians who think that all functions are continuous. One way of explaining this is to show that all computable functions are continuous. The point not appreciated by many (even experts) is that the truth of this claim depends on what programming language we use.

→ continue reading (40 comments)

In constructive mathematics even very small sets can be quite a bit more interesting than in classical mathematics. Since you will not believe me that sets with at most one element are very interesting, let us look at the set of truth values, which has “two” elements.

→ continue reading (18 comments)

What constructive mathematics actually says about the law of excluded middle. → continue reading (8 comments)