In 1890 Giuseppe Peano discovered a square-filling curve, and a year later David Hilbert published his variation. In those days people did not waste readers' attention with dribble – Peano explained it all on 3 pages, and Hilbert on just 2 pages, with a picture!

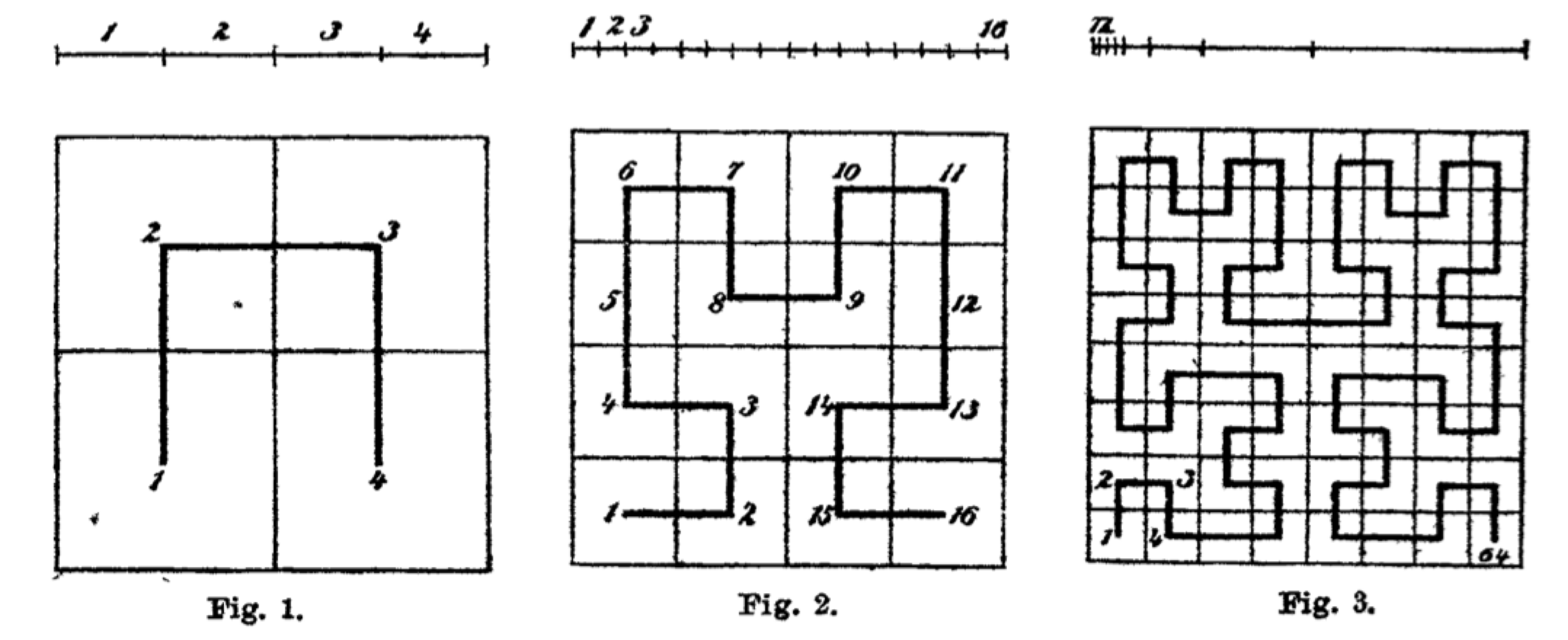
But are these constructive square-filling curves?

→ continue reading

I have not written a blog post in a while, so I decided to write up a short observation about truth values in intuitionistic logic which sometimes seems a bit puzzling.

Let $\Omega$ be the set of truth values (in Coq this would be the setoid whose underlying type is $\mathsf{Prop}$ and equality is equivalence $\leftrightarrow$, while in HoTT it is the h-propostions). Call a truth value $p : \Omega$ intermediate if it is neither true nor false, i.e., $p \neq \bot$ and $p \neq \top$. Such a “third” truth value $p$ is proscribed by excluded middle.

The puzzle is to explain how the following two facts fit together:

1. “There is no intermediate truth value” is an intuitionistic theorem.
2. There are models of intuitionistic logic with many truth values.

→ continue reading (6 comments)

I am not sure whether to call this one a constructive gem or stone. I suppose it is a matter of personal taste. I think it is a gem, albeit a very unusual one: there is a topos in which $\mathbb{N}^\mathbb{N}$ can be embedded into $\mathbb{N}$.

→ continue reading (3 comments)

The following argument is often cited as an example of the necessity of the law of excluded middle and classical logic. We are supposed to demonstrate the existence of two irrational numbers $a$ and $b$ such that their power $a^b$ is rational. By the law of excluded middle, $\sqrt{2}^{\sqrt{2}}$ is rational or not. If it is rational, take $a = b = \sqrt{2}$, otherwise take $a = \sqrt{2}^{\sqrt{2}}$ and $b = \sqrt{2}$. In either case $a^b$ is rational. Let us think about this for a moment, from constructive point of view.

→ continue reading (18 comments)

In the last constructive gem we studied the exponential $2^\mathbb{N}$ and its isomorphic copies. This time we shall compute the double exponential $2^{2^\mathbb{N}}$ and even write some Haskell code.

→ continue reading (4 comments)

Constructive gems are usually not about particular results, because all constructive results can be proved classically as well, but rather about the method and the way of thinking. I demonstrate a constructive proof which can be reused in three different settings (set theory, topology, computability) because constructive mathematics has many different interpretations.

→ continue reading (28 comments)

I promise I will post a constructive gem soon. This constructive stone came up as a reaction to the cardinality of finite sets stone. I show that inhabited sets of natural numbers need not have minima, constructively.

→ continue reading

Cardinality of sets in constructive mathematics is not as well behaved as in classical mathematics. Cardinalities of finite sets are not natural numbers, and cardinalities are not linearly ordered.

→ continue reading (13 comments)

Just like in real life, constructive stones are easier to find than constructive gems, so let me start the series with a stone about constructive finite sets.

Two girl one cup
→ continue reading (3 comments)

In various mathematical forums, mostly those of a logical flavor, I regularly see people asking basic questions about constructive mathematics. I also see misconceptions about constructive mathematics. I shall make a series of posts, _Constructive Gems and Stone_s, which will answer basic questions about constructive mathematics, and will hopefully help fix wrong ideas about constructive mathematics.

A constructive gem is something nice about constructive mathematics that makes you want to know more about it. In contrast, a constructive stone is a complication in constructive mathematics which does not exist in the classical counterpart.

Here we go! The first one is about finite sets.

→ continue reading