Space-filling curves, constructively
- 30 January 2024
- Constructive math, Gems and stones
In 1890 Giuseppe Peano discovered a square-filling curve, and a year later David Hilbert published his variation. In those days people did not waste readers' attention with dribble – Peano explained it all on 3 pages, and Hilbert on just 2 pages, with a picture!
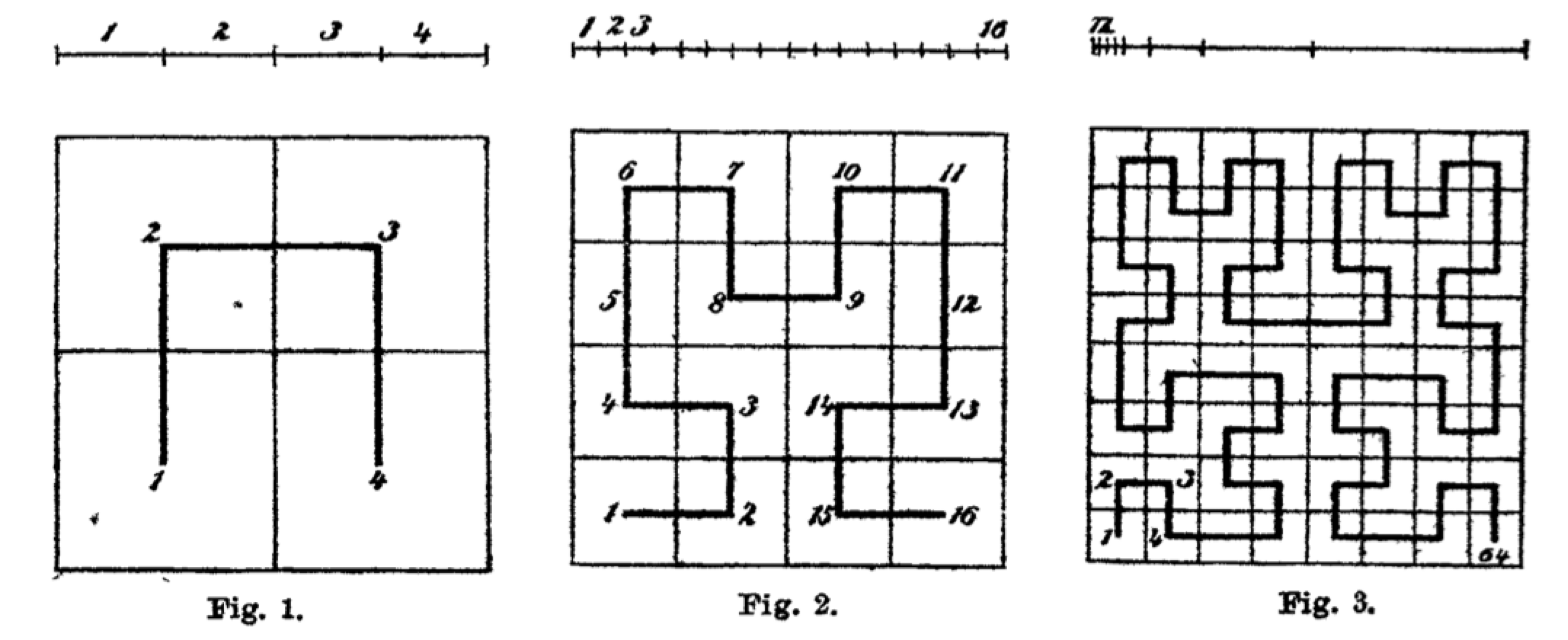
But are these constructive square-filling curves?
→ continue readingOn indefinite truth values
- 13 August 2023
- Logic
In a discussion following a MathOverflow answer by Joel Hamkins, Timothy Chow and I got into a chat about what it means for a statement to “not have a definite truth value”. I need a break from writing the paper on countable reals (coming soon in a journal near you), so I thought it would be worth writing up my view of the matter in a blog post.
→ continue readingVariations on Weihrauch degrees (CiE 2023)
- 28 July 2023
- Talks, Computation
I gave a talk “Variations on Weihrauch degrees” at Computability in Europe 2023, which took place in Tbilisi, Georgia. The talk was a remote one, unfortunately. I spoke about generalizations of Weihrauch degrees, a largely unexplored territory that seems to offer many opportunities to explore new directions of research. I am unlikely to pursue them myself, but will gladly talk with anyone who is interested in doing so.
Slides: CiE-2023-slides.pdf.
Continuity principles and the KLST theorem
- 19 July 2023
- Constructive math, Synthetic computatibility
On the occasion of Dieter Spreen's 75th birthday there will be a Festschrift in the Journal of Logic and Analysis. I have submitted a paper “Spreen spaces and the synthetic Kreisel-Lacombe-Shoenfield-Tseitin theorem”, available as a preprint arXiv:2307.07830, that develops a constructive account of Dieter's generalization of a famous theorem about continuity of computable functions. In this post I explain how the paper fits into the more general topic of continuity principles.
→ continue readingIsomorphism invariance and isomorphism reflection in type theory (TYPES 2023)
- 15 June 2023
- Talks, Type theory
At TYPES 2023 I had the honor of giving an invited talk “On Isomorphism Invariance and Isomorphism Reflection in Type Theory” in which I discussed isomorphism reflection, which states that isomorphic types are judgementally equal. This strange principle is consistent, and it validates some fairly strange type-theoretic statements.
Here are the slides with speaker notes and the video recording of the talk.
→ continue readingFormalizing invisible mathematics
- 13 February 2023
- Talks
I am at the Machine assisted proofs workshop at the UCLA Institute for Pure and Applied Mathematics, where I am about to give a talk on “Formalizing invisible mathematics”.
Here are the slides with speaker notes and the video recording of the talk.
→ continue readingExploring strange new worlds of mathematics
- 10 February 2023
- Talks, Constructive math
On February 10, 2023, I gave my Levi L. Conant Lectur Series talk “Exploring strange new worlds of mathematics”, at the math department of Worcester Polytechnic Institute. Here are the slides with speaker notes and the video recording of the talk.
→ continue readingHappy birthday, Dana!
- 11 October 2022
- News
Today Dana Scott is celebrating the 90th birthday today. Happy birthday, Dana! I am forever grateful for your kindness and the knowledge that I received from you. I hope to pass at least a part of it onto my students.
On the occasion Steve Awodey assembled selected works by Dana Scott at CMU-HoTT/scott repository. It is an amazing collection of papers that had deep impact on logic, set theory, computation, and programming languages. I hope in the future we can extend it and possibly present it in better format.
As a special treat, I recount here the story the invention of the famous $D_\infty$ model of the untyped $\lambda$-calculus. I heard it first when I was Dana's student. In 2008 I asked Dana to recount it in the form of a short interview.
→ continue reading (1 comment)One syntax to rule them all
- 20 May 2022
- Talks
I am at the Syntax and Semantics of Type Theory workshop in Stockholm, a kickoff meeting for WG6 of the EuroProofNet COST network, where I am giving a talk “One syntax to rule them all” based on joint work with Danel Ahman.
→ continue readingTwo new doctors!
- 12 January 2022
- News
Within a month two of my students defended their theses: Dr. Anja Petković Komel just before Christmas, and Dr. Philipp Haselwarter just yesterday. I am very proud of them. Congratulations!
→ continue reading