Mathematics and Computation

Today I lectured about the Hydra game by Laurence Kirby and Jeff Paris (Accessible Independence Results for Peano Arithmetic, Kirby and Paris, Bull. London Math. Soc. 1982; 14: 285-293). For the occasion I implemented the game in Java. I am publishing the code for anyone who wants to play, or use it for teaching.

About the game

A hydra is a finite tree, with a root at the bottom. The object of the game is to cut down the hydra to its root. At each step, you can cut off one of the heads, after which the hydra grows new heads according to the following rules:

• If you cut off a head growing out of the root, the hydra does not grow any new heads.

• Suppose you cut off a head like this:
  

  
  
  
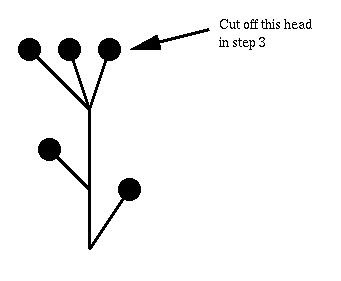  Delete the head and its neck. Descend down by 1 from the node at which the neck was attached. Look at the subtree growing from the connection through which you just descended. Pick a natural number, say 3, and grow that many copies of that subtree, like this: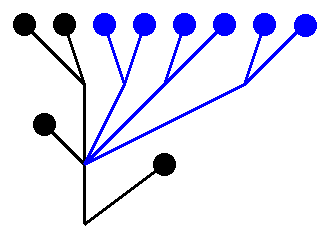
  
  
  

My program grows `n` copies at step `n` of the game, which is one possible variant of the game. There are spoilers ahead, so before you read on you should play the game with the Hydra applet (your browser must support Java) and try to win. Is it possible to win? How should you play to win?

Here is a surprising fact:

Theorem 1: You cannot lose!

The proof uses ordinal numbers. To each hydra we assign an ordinal number:

• A head gets the number `0`.
• Suppose a node `x` has sub-hydras `H_1`, …, `H_n` growing from it. To each sub-hydra we assign its ordinal recursively and order the ordinals in descending order: `alpha_1 >= alpha_2 >= … >= alpha_n`. The ordinal assigned to the node `x` is `omega^(alpha_1) + omega^(alpha_2) + … + omega^(alpha_n)`. For example, the ordinal corresponding to the hydra from the first picture above is `omega^(omega^3 + 1) + 1`. The hydra in the second picture gets the ordinal `omega^(4 omega^2 + 1) + 1`.
• By chopping off a head we strictly decrease the ordinal. Because there are no infinite strictly descending sequences of ordinals, the hydra will eventually die, no matter how you chop off heads.

But Theorem 1 is not the punchline. The punchline is this:

Theorem 2 (Kirby and Paris): Any proof technique that proves Theorem 1 is strong enough to prove that Peano arithmetic is consistent.

Consistency of Peano arithmetic is Hilbert’s second problem, which was solved by Gentzen in 1936.

Download the program

The program is written in Java and is available freely under the BSD License. You may:

• Download the source code hydra.zip as an Eclipse project.
• Download a JAR file hydra.jar, suitable for running on your computer as a stand-alone application, for which you need Java Runtime Environment (JDK will do as well, of course).
• Try the game online.